ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ - урок 2

Цели: ввести понятие ромба и квадрата; изучить их свойства.

Ход урока

I. Проверка домашнего задания.

1. АD АВ, ВС АВ (по условию), тогда АD || ВС (как два перпендикуляра к одной прямой).

2. АВ ВС, СD ВС (по условию), тогда АВ || СD (как два перпендикуляра к одной прямой).

3. Так как АD || ВС и АВ || СD, тогда АВСD – параллелограмм (по определению).

4. D = В (как противолежащие углы параллелограмма).

5. В параллелограмме АВСD: А = В = С = D = 90°, значит, АВСD – прямоугольник (по определению).

Выполнить задания (устно):

1) Найдите боковую сторону равнобедренного треугольника, высота которого равна 6 см, а угол при вершине равен 120°.

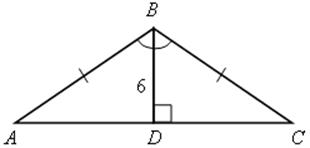
А = 30°, АВ = 2ВD = 12 (см).

2) Диагонали параллелограмма взаимно перпендикулярны.

Докажите, что все его стороны равны.

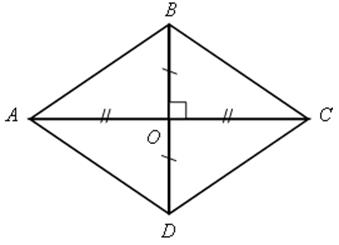
ВОС = DОС = ВОА = DОА по двум катетам.

Имеем АВ = ВС = DС = АD.

II. Изучение нового материала.

1. Определение ромба.

2. Так как ромб – параллелограмм, то какими свойствами он обладает?

3. Какими особыми свойствами обладает ромб?

4. Доказательство свойств ромба:

а) диагонали ромба взаимно перпендикулярны;

б) диагонали являются биссектрисами углов.

5. Будут ли верны обратные утверждения? Докажите.

6. Определение квадрата как прямоугольника, у которого все стороны равны.

7. Определение квадрата как ромба, у которого все углы прямые.

8. Так как квадрат является ромбом и прямоугольником, то он обладает их свойствами. Перечислите их.

III. Решение задач.

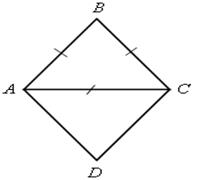
№ 405 (а).

а) АВ = ВС = АС, АВС – равносторонний, А = В = С = 60° в ромбе АВС = 60°, ВАD = 120°.

№ 410 (а, б) признаки квадрата.

IV. Итоги урока.

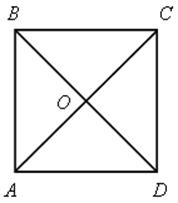
Свойства ромба

АВСD – ромб		АВ || CD, ВC || АD, А = С, В = D, АО = ОС, ВО = ОD	свойства параллелограмма
		АВ = ВC = CД = АD АС ВD АС – биссектриса А ВD – биссектриса В	все стороны равны диагонали перпендикулярны каждая диагональ – биссектриса углов ромба
АВСD – ромб

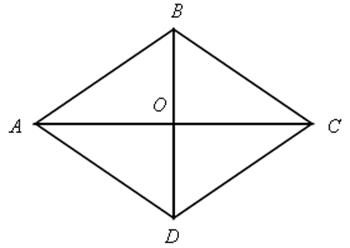
Признаки ромба

АВ = ВС = СD = АD		АВСD – ромб
АВСD – параллелограмм АС ВD		АВСD – ромб
АВСD – параллелограмм и АС – биссектриса А		АВСD – ромб

Свойства квадрата

АВСD – квадрат
АВ || CD, ВC || АD АВ = ВC = CD = АD А = В = C = D = 90° АО = ВО = CО = DО АС ВD АС, ВD, СА, DВ – биссектриса угла		все стороны равны все углы прямые отрезки диагоналей равны диагонали перпендикулярны каждая диагональ является биссектрисой угла

Признаки квадрата

Для того чтобы доказать, что данный четырехугольник является квадратом, можно:

џ доказать, что четырехугольник является прямоугольником с равными сторонами;

џ доказать, что четырехугольник является ромбом с прямыми углами.

Домашнее задание: вопросы 14–15, с. 115; №№ 405 (б), 409.

АВСD – ромб.

Найти: ВАD.

Дано: АВСD – квадрат.

Доказать: А1В1С1D1 – прямоугольник.