Уроки-конспекты по Геометрии 8 класс
ТЕОРЕМА ПИФАГОРА - урок 2
Цель: рассмотреть решение задач с помощью теоремы Пифагора.
Ход урока
I. Проверка домашнего задания.
Записать теорему Пифагора для треугольников.
1)
|
2)
|
3) АВСD – ромб.
|
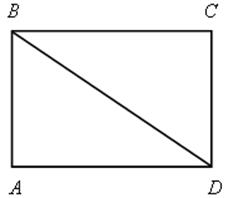
4) АВСD – прямоугольник.
|
5)
|
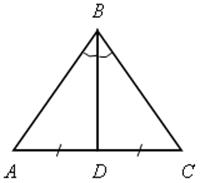
6) DЕ – высота.
|
II. Решение задач.
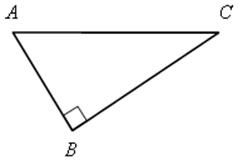
№ 485.
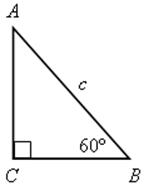
1) ![]() А = 90° – 60° = 30°.
А = 90° – 60° = 30°.
2) СВ = ![]() , как катет, лежащий против угла в 30°.
, как катет, лежащий против угла в 30°.
3) По теореме Пифагора
АВ2 = АС2 + СВ2, АС2 = АВ2 – СВ2
АС2 = с2 – ![]() =
= ![]() , АС =
, АС = 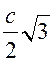 .
.
Решить устно:
На какое расстояние надо отодвинуть от стены дома нижний конец лестницы длиною 17 м, чтобы верхний конец ее достал до слухового окна, находящегося на высоте 15 м от поверхности земли.
Решение
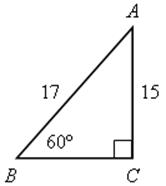
![]() АВС прямоугольный.
АВС прямоугольный.
По теореме Пифагора
АВ2 = АС2 + ВС2,
ВС2 = АВ2 – АС2,
ВС = ![]() =
= ![]() = 8 (м).
= 8 (м).
№ 488 (а).
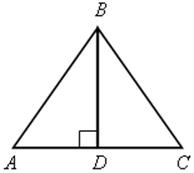
1) ВD – высота и медиана равностороннего треугольника, поэтому DС = 3 см.
2) ![]() ВСD – прямоугольный. По теореме Пифагора имеем ВС2 = ВD2 + DС2, ВD2 = ВС2 – DС2, ВD =
ВСD – прямоугольный. По теореме Пифагора имеем ВС2 = ВD2 + DС2, ВD2 = ВС2 – DС2, ВD = ![]() =
=![]() .
.
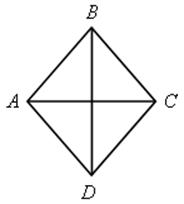
№ 493.
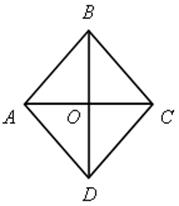
Решение
1) По свойству диагоналей ромба ВО = ОD = 12 см, АО = ОС = 5 см.
2) По свойству ромба ![]() ВОС = 90°.
ВОС = 90°.
3) По теореме Пифагора в ![]() ВОС имеем ВС2 = ВО2 + ОС2.
ВОС имеем ВС2 = ВО2 + ОС2.
ВС = ![]() = 13 (см).
= 13 (см).
4) SАВСD = ![]() ВD · АС.
ВD · АС.
SАВСD = ![]() · 24 · 10 = 120 (см2).
· 24 · 10 = 120 (см2).
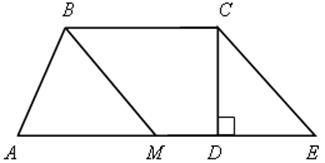
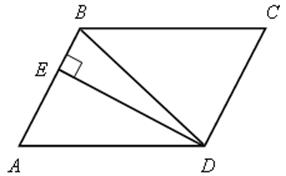
№ 495 (а).
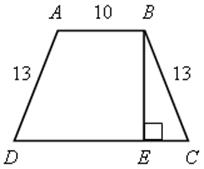
1) ВЕ – высота трапеции.
![]() ВСЕ – прямоугольный.
ВСЕ – прямоугольный.
2) По теореме Пифагора имеем в ![]() ВСЕ:
ВСЕ:
ВС2 = ЕС2 + ВЕ2, ВЕ2 = ВС2 – ЕС2.
3) ЕС = 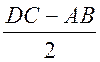 по свойству равнобокой трапеции ЕС =
по свойству равнобокой трапеции ЕС = 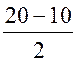 = 5 (см).
= 5 (см).
4) ВЕ = ![]() = 12 (см).
= 12 (см).
III. Итоги урока.
При решении задач с применением теоремы Пифагора нужно:
1) указать прямоугольный треугольник;
2) записать для него теорему Пифагора;
3) выразить неизвестную сторону через две другие;
4) подставив известные значения, вычислить неизвестную сторону.
Домашнее задание: №№ 486 (а), 487, 494, 495 (б).
Для желающих.
Задачи древнекитайского ученого Цзинь Киу-чау, 1250 лет до н. э.
1. Бамбуковый ствол 9 футов высотой переломлен бурей так, что если верхнюю часть его нагнуть к земле, то верхушка коснется земли на расстоянии 3 футов от основания ствола. На какой высоте переломлен ствол?
Решение
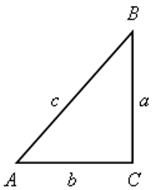
а + с = 9 футов, b = 3 фута, с = 9 – а.
![]() АВС – прямоугольный.
АВС – прямоугольный.
По теореме Пифагора
с2 = а2 + b2,
(9 – а)2 = а2 + 32,
81 – 18а + а2 = а2 + 9.
18а = 72,
а = 4.
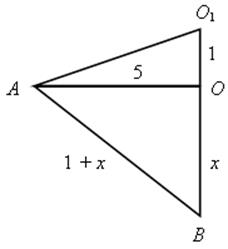
2. В центре квадратного пруда, имеющего 10 футов в длину и ширину, растет тростник, возвышающийся на 1 фут над поверхностью воды. Если его пригнуть к берегу, к середине стороны пруда, то он достигнет своей верхушкой берега. Какова глубина пруда?
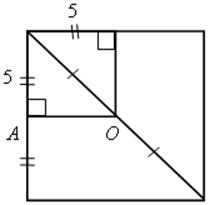
Решение
АО = 5 футов – расстояние от центра квадрата до середины стороны.
АВ = О1В
![]() ОАВ – прямоугольный.
ОАВ – прямоугольный.
По теореме Пифагора
АВ2 = АО2 + ОВ2.
Пусть ОВ = х футов, тогда АВ = (1 + х) футов. Имеем (1 + х)2 = 52 + х2,
1 + 2х + х2 = 25 + х2,
х = 12,
ОВ = 12 футов.