КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ

Цель: рассмотреть возможные случаи взаимного расположения прямой и окружности.

Ход урока

I. Анализ контрольной работы.

II. Решение задач.

Решить устно:

1. Радиус окружности 5 см.

Найдите расстояние от центра окружности до прямой, содержащей хорду, равную 8 см.

d = = 3 (см).

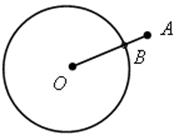
2. Найдите расстояние от точки А до ближайшей к ней точки окружности с центром О радиуса r, если а) ОА = 12 см, r = 8 см; б) АО = 6 см, r = 8 cм.

а) АВ = ОА – r; АВ = 12 – 8 = 4 (см).

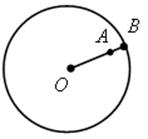
б) АВ = r – ОА; АВ = 8 – 6 = 2 (см).

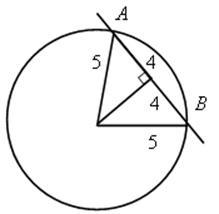
3. Докажите, что АВ < АВ1, используя неравенство треугольника.

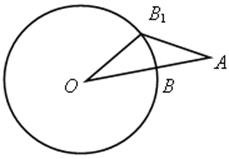
Имеем ОА < ОВ1 + АВ1

ОВ + АВ < ОВ1 + АВ1, так как ОВ = ОВ1 = r, то АВ < АВ1.

III. Изучение нового материала.

Изложить весь материал п. 68 в виде небольшой лекции.

При обосновании утверждения о том, что прямая и окружность не могут иметь более двух общих точек, полезно сделать рисунок.

IV. Закрепление изученного материала.

Решить № 631 (а, г, д) – устно, № 632.

№ 632.

Решение

Дано: окружность с центром в точке О и радиусом r, ОА < r.

Доказать: любая прямая р, проходящая через точку А – секущая.

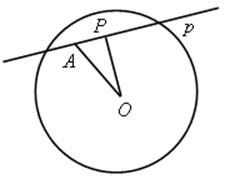
1) Через точку А проведем произвольную прямую р, найдем расстояние от точки О до прямой р. Для этого проведем ОР р.

2) АОР, Р = 90°. Катет ОР меньше гипотенузы АО, АО < r по условию, значит, ОР < r , следовательно, прямая р – секущая. В случае если АО р, но АО < r, прямая р также является секущей.

V. Итоги урока.

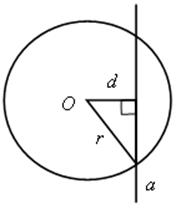
d < r, прямая а – секущая.

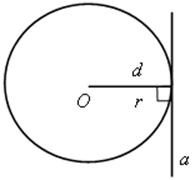
d = r, прямая а имеет с окружностью одну общую точку.

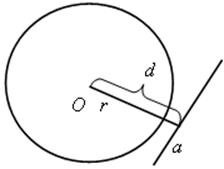
d > r, прямая а не имеет общих точек с окружностью.

Домашнее задание: вопросы 1, 2, с. 187; № 631 (б, в) – устно, № 633; сделать работу над ошибками в контрольной работе.