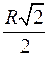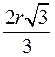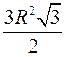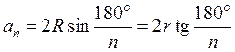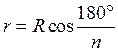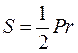Поурочные разработки по геометрии 9 класс
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности - ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА
Цели: выработать у учащихся умение выводить формулы, связывающие радиус описанной окружности и радиус вписанной окружности со стороной а правильного n-угольника, на их основе научить учащихся получать формулы для вычисления аn через R и r и конкретизировать их для случая n = 3, n = 4, n = 6, выработать навыки применения полученных знаний при решении задач.
Ход урока
I. Анализ самостоятельной работы.
II. Изучение нового материала.
1. Вывод формул (1–6) из пункта 108 учебника учащиеся проводят самостоятельно под руководством учителя по заранее заготовленному на доске рисунку 308.
2. После вывода формул для правильного n-угольника рассмотреть их частные случаи для n = 3, n = 4, n = 6.
3. Выведенные формулы оформить в виде таблицы, которую учащиеся записывают в тетради:
n |
а |
R |
r |
S |
S |
|
3 |
|
|
2r |
|
|
|
4 |
|
2r |
|
|
2R2 |
4r2 |
6 |
R |
|
|
|
|
|
n |
|
|
|
|||
Эту таблицу учитель оформляет как настенную на картоне.
III. Закрепление изученного материала (решение задач).
1. Решение учащимися задач на непосредственное применение выведенных формул:
1) В окружность радиуса R = 12 вписан правильный n-угольник. Определите его сторону и периметр, если: а) n = 3; б) n = 4; в) n = 6.
2) Около окружности радиуса r = 6 описан правильный n-угольник. Определите его сторону и периметр, если: а) n = 3; б) n = 4; в) n = 6.
3) Для правильного n-угольника со стороной а = 6 см найдите радиус описанной около него окружности, если: а) n = 3; б) n = 4; в) n = 6.
2. Решить задачу № 1089.
Решение
Р = 18 см; а = 18 : 3 = 6 (см);
а3 = R![]() ;
; ![]() R =
R =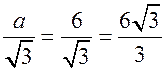 = 2
= 2![]() (см); а4 = R
(см); а4 = R![]() = 2
= 2![]() ∙
∙ ![]() = 2
= 2![]() (см).
(см).
Ответ: 2![]() см.
см.
3. Решить задачу № 1090.
Решение
а3 = 3 см; R =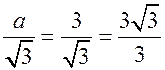
![]() (см); d = 2R = 2
(см); d = 2R = 2![]() (см).
(см).
ответ: 2![]() см.
см.
4. Решить задачу № 1092.
Решение
Р = 48 см; а6 = 48 : 6 = 8 (см); а6 = = 8 (см); r =
= 8 (см); r =![]() = 4
= 4![]() (см); а4 = 2r = 8
(см); а4 = 2r = 8![]() (см) ; р = 4 ∙ а4 = 8
(см) ; р = 4 ∙ а4 = 8![]() ∙ 4 = 32
∙ 4 = 32![]() (см).
(см).
Ответ: 32![]() см.
см.
5. Решить задачу:
Правильный треугольник АВС вписан в окружность с центром О и радиусом 8 см. На стороне этого треугольника построен квадрат. Определите радиус окружности, описанной около квадрата.
IV. Итоги урока.
Задание на дом: изучить материал пункта 108; решить задачи №№ 1087, 1088, 1094 (а, б).