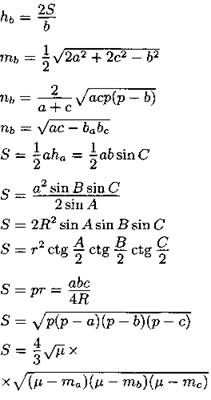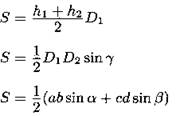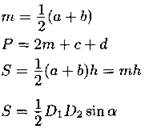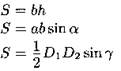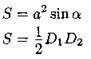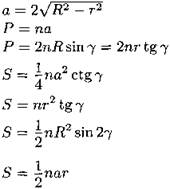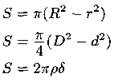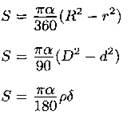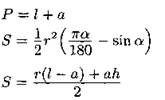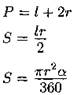Математика 9 класс подготовка к ГИА
Геометрия - Краткий теоретический справочник
Параллельные прямые.
Свойства и признаки параллельных прямых.
1. Аксиома параллельных. Через данную точку можно провести не более одной прямой, параллельной данной.
2. Если две прямые параллельны одной и той же прямой, то они параллельны между собой.
3. Две прямые, перпендикулярные одной и той же прямой, параллельны.
4. Если две параллельные прямые пересечь третьей, то образованные при этом внутренние накрест лежащие углы равны, соответственные углы равны, односторонние углы в сумме составляют 180°.
5. Если при пересечении двух прямых третьей образуются равные внутренние накрест лежащие углы, то прямые параллельны.
6. Если при пересечении двух прямых третьей образуются равные соответственные углы, то прямые параллельны.
7. Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Теорема Фалеса.
Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие вторую сторону угла, то на второй стороне угла отложатся также равные отрезки.
Теорема о пропорциональных отрезках.
Параллельные прямые, пересекающие стороны угла, высекают на них пропорциональные отрезки.
Треугольник.
Признаки равенства треугольников.
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.
3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то треугольники равны.
Признаки равенства прямоугольных треугольников.
1. По двум катетам.
2. По катету и гипотенузе.
3. По гипотенузе и острому углу.
4. По катету и острому углу.
Теорема о сумме углов треугольника и следствия из неё.
1. Сумма углов треугольника равна 180°.
2. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
3. Сумма углов выпуклого п-угольника равна 180°(n — 2).
4. Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые (на рис. 16 ∠1 =∠2).
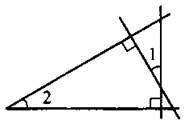
Рис. 16
5. Угол между биссектрисами смежных углов равен 90°.
6. Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны (на рис. 17 прямые а || b, m ⊥ n).
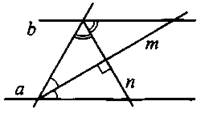
Рис. 17
Основные свойства и признаки равнобедренного треугольника.
1. Углы при основании равнобедренного треугольника равны.
2. Если два угла треугольника равны, то он равнобедренный.
3. В равнобедренном треугольнике медиана, биссектриса и высота, проведённые к основанию, совпадают.
4. Если в треугольнике совпадает любая пара отрезков из тройки: медиана, биссектриса, высота, то он является равнобедренным.
Неравенство треугольника и следствия из него.
1. Сумма двух сторон треугольника больше третьей стороны.
2. Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.
3. Против большего угла треугольника лежит большая сторона.
4. Против большей стороны треугольника лежит больший угол.
5. Гипотенуза прямоугольного треугольника больше катета.
6. Если из одной точки проведены к прямой перпендикуляр и наклонные, то
1) перпендикуляр короче наклонных;
2) большей наклонной соответствует большая проекция и наоборот.
Средняя линия треугольника.
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Теорема о средней линии треугольника. Средняя линия треугольника параллельна стороне треугольника и равна её половине.
Теоремы о медианах треугольника.
1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.
2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный.
3. Медиана делит треугольник на два равновеликих (равных по площади) треугольника.
4. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
Свойство серединных перпендикуляров к сторонам треугольника.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.
Теорема о высотах треугольника.
Прямые, содержащие высоты треугольника, пересекаются в одной точке.
Теорема о биссектрисах треугольника.
Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
Свойство биссектрисы треугольника.
Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам (на рис. 18 выполняется ![]() ).
).
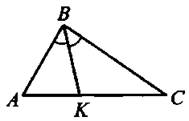
Рис. 18
Признаки подобия треугольников.
1. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключённые между этими сторонами, равны, то треугольники подобны.
3. Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.
Площади подобных треугольников.
1. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
2. Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.
Прямоугольный треугольник.
1. В прямоугольном треугольнике (см. рис. 19) тригонометрические функции задаются следующим образом:
![]()
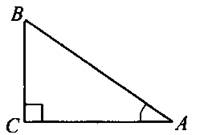
Рис. 19
2. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла (см. рис. 19, ВС = АВ ∙ sin ∠A,ВС = АВ ∙ cos ∠B).
3. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к этому катету острого угла (см. рис. 19, ВС = АС ∙ tg∠A, ВС = АС ∙ctg ∠B).
4. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
5. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30°.
6. ![]() где а, b — катеты, а с — гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружности соответственно.
где а, b — катеты, а с — гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружности соответственно.
Теорема Пифагора и теорема, обратная теореме Пифагора.
1. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
2. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный.
Средние пропорциональные в прямоугольном треугольнике.
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.
Метрические соотношения в треугольнике.
1. Теорема синусов (см. рис. 20).
![]()
2. Теорема косинусов (см. рис. 20).
![]()
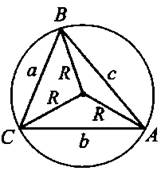
Рис. 20
3. Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Формулы площади треугольника.
Пусть дан треугольник (см. рис. 21), r и R — радиусы его вписанной и описанной окружностей (соответственно), ![]() — полупериметр.
— полупериметр.
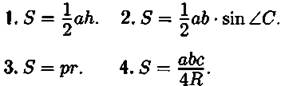
5. Формула Герона: ![]()
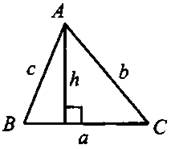
Рис. 21
Элементы равностороннего треугольника. Пусть h, S, r, R — высота, площадь, радиусы вписанной и описанной окружностей равностороннего треугольника со стороной а. Тогда ![]()
Параллелограмм.
Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма.
1. Диагональ разбивает параллелограмм на два равных треугольника.
2. Противоположные стороны параллелограмма попарно равны.
3. Противоположные углы параллелограмма попарно равны.
4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.
Свойство середин сторон четырёхугольника.
Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.
Прямоугольник.
Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника.
1. Диагонали прямоугольника равны.
2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.
Квадрат.
Квадратом называется прямоугольник, все стороны которого равны.
Ромб.
Ромбом называется четырёхугольник, все стороны которого равны.
Свойства и признаки ромба.
1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его углы пополам.
3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
Трапеция.
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
1. Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Отрезок, соединяющий середины диагоналей трапеции, равен полу- разности её оснований.
Замечательное свойство трапеции.
Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция.
Трапеция называется равнобедренной, если её боковые стороны равны.
Свойства и признаки равнобедренной трапеции.
1. Углы при основании равнобедренной трапеции равны.
2. Диагонали равнобедренной трапеции равны.
3. Если углы при основании трапеции равны, то она равнобедренная.
4. Если диагонали трапеции равны, то она равнобедренная.
5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.
Формулы площади четырёхугольника.
1. Площадь параллелограмма равна произведению основания на высоту.
2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
3. Площадь прямоугольника равна произведению двух его соседних сторон.
4. Площадь ромба равна половине произведения его диагоналей.
5. Площадь трапеции равна произведению полусуммы оснований на высоту.
6. Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
7. Формула Герона для четырёхугольника, около которого можно описать окружность:
![]()
где a, b, c, d — стороны этого четырёхугольника, р — полупериметр,a S — площадь.
Подобные фигуры.
1. Отношение соответствующих линейных элементов подобных фигур равно коэффициенту подобия.
2. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Правильный многоугольник.
Пусть an — сторона правильногоn-угольника, а rn и Rn — радиусы вписанной и описанной окружностей. Тогда:
![]()
Окружность.
Окружностью называется геометрическое место точек плоскости, удалённых отданной точки, называемой центром окружности, на одно и то же положительное расстояние.
Основные свойства окружности.
1. Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею дуги пополам.
2. Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
3. Серединный перпендикуляр к хорде проходит через центр окружности.
4. Равные хорды удалены от центра окружности на равные расстояния.
5. Хорды окружности, удалённые от центра на равные расстояния, равны.
6. Окружность симметрична относительно любого своего диаметра.
7. Дуги окружности, заключённые между параллельными хордами, равны.
8. Из двух хорд больше та, которая менее удалена от центра.
9. Диаметр есть наибольшая хорда окружности.
Замечательные свойства окружности.
1. Геометрическое место точек М, из которых отрезок АВ виден под прямым углом (∠AMВ — 90°), есть окружность с диаметром АВ без точек А а В.
2. Геометрическое место точек М, из которых отрезок АВ виден под острым углом (∠AMВ < 90°), есть внешность круга с диаметром АВ без точек прямой АВ.
3. Геометрическое место точек М, из которых отрезок АВ виден под тупым углом (∠AMВ > 90°), есть внутренность круга с диаметром АВ без точек отрезка АВ.
4. Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных окружностей (без концов этих дуг).
Касательная к окружности.
Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.
1. Касательная перпендикулярна радиусу, проведённому в точку касания.
2. Если прямая о, проходящая через точку на окружности, перпендикулярна радиусу, проведённому в эту точку, то прямая а — касательная к окружности.
3. Если прямые, проходящие через точку М, касаются окружности в точках А и В, то МА = МВ и ∠АМО = ∠ВМО, где точка О — центр окружности (см. рис. 22).
4. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
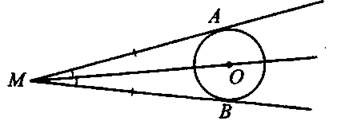
Рис. 22
Касающиеся окружности.
Говорят, что две окружности касаются, если они имеют единственную общую точку (точку касания).
1. Точка касания двух окружностей лежит на их линии центров.
2. Окружности радиусов r иR с центрами О1 и О2 касаются внешним образом тогда и только тогда, когдаR + r = О1О2.
3. Окружности радиусов r и R (r < R) с центрами О1 и О2 касаются внутренним образом тогда и только тогда, когдаR —r = О1О2.
4. Окружности с центрами О1 и О2 касаются внешним образом в точке К (см. рис. 23). Некоторая прямая касается этих окружностей в различных точках А и В и пересекается с общей касательной, проходящей через точку К, в точке С. Тогда∠AKB = 90° и∠O1CO2 = 90°.
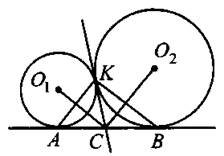
Рис. 23
5. Отрезок общей внешней касательной к двум касающимся окружностям радиусов r и R равен отрезку общей внутренней касательной, заключённому между общими внешними. Оба эти отрезка равны ![]() (см. рис. 24: АС =BD =MN =
(см. рис. 24: АС =BD =MN = ![]() ).
).
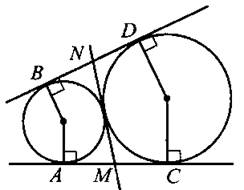
Рис. 24
Углы, связанные с окружностью.
1. Величина дуги окружности равна величине центрального угла, на неё опирающегося.
2. Вписанный угол равен половине угловой величины дуги, на которую он опирается.
3. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
4. Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами (см. рис. 25: ![]() ).
).
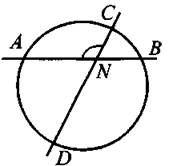
Рис. 25
5. Угол между двумя секущими, пересекающимися вне круга, равен полуразности дуг, высекаемых секущими на окружности (см. рис. 26: ![]() ).
).
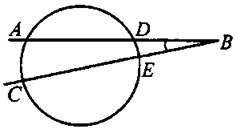
Рис. 26
6. Угол между касательной и хордой, проведённой из точки касания, равен половине угловой величины дуги, высекаемой на окружности этой хордой (см. рис. 27: ![]() ).
).
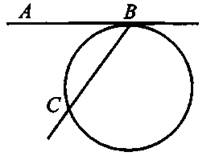
Рис. 27
Свойства хорд окружности.
1. Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.
2. Произведения длин отрезков хорд АВ и CD окружности, пересекающихся в точке Е, равны, то есть АЕ ∙ ЕВ = СЕ ∙ED (см. рис. 28).
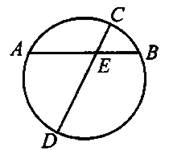
Рис. 28
Вписанные и описанные окружности.
1. Центры вписанной и описанной окружностей правильного треугольника совпадают.
2. Центр окружности, описанной около прямоугольного треугольника, — это середина гипотенузы.
3. Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны.
4. Если четырёхугольник можно вписать в окружность, то сумма его противоположных углов равна 180°.
5. Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
6. Если в трапецию можно вписать окружность, то боковая сторона трапеции видна из центра окружности под прямым углом.
7. Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону
8. Если в многоугольник можно вписать окружность, то его площадь равна произведению полупериметра многоугольника на радиус этой окружности.
Теорема о касательной и секущей и следствие из нее.
1. Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной (см. рис. 29: АВ2 = AD ∙ АС).
2. Произведение всей секущей на её внешнюю часть для данной точки и данной окружности постоянно.
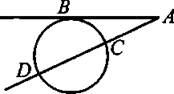
Рис. 29
Длина окружности радиуса R равна2πR.
Площадь круга радиуса R равна πR2.
Основные формулы
Далее S — площадь фигуры, Р — периметр, р — полупериметр.
|
Чертежи |
Обозначения |
Формулы |
|
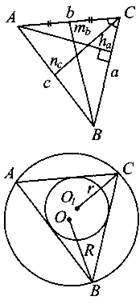
Треугольник
|
а, b, с — стороны; А, В, С — противолежащие им углы; ha, hb, hc высоты, проведённые к соответствующим сторонам; na, nb, nc — биссектрисы, проведённые к соответствующим сторонам; bа и bс — отрезки, на которые делится биссектрисой сторона b; ma, mb, mc — медианы, проведённые к соответствующим сторонам;
R — радиус описанной окружности; r — радиус вписанной окружности. |
|
|
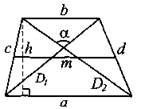
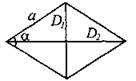
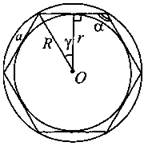
Четырёхугольник
|
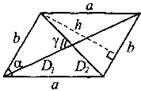
а, b, с, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h1, h2 — длины перпендикуляров, опущенных на диагональD1; а, β — два противолежащих угла четырёхугольника. |
|
|
Трапеция
|
а, b — основания; с, d — боковые стороны; D1, D2 — диагонали; α — угол между диагоналями; m — средняя линия; h — высота. |
|
|
Параллелограмм
|
а, b — стороны; h — расстояние между сторонамиb; α — угол параллелограмма; D1, D2 — диагонали; γ — угол между диагоналями. |
|
|
Ромб
|
a — сторона; α — угол ромба; D1, D2 —диагонали. |
|
|
Правильный многоугольник
|
n — число сторон; a — сторона; R — радиус описанной окружности; r — радиус вписанной окружности; α = 180° - 2γ — угол многоугольника |
|
|
Круг
|
R — радиус; l — длина окружности. |
|
|
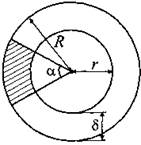
Круговое кольцо
|
r — внутренний радиус; R — наружный радиус; d — внутренний диаметр; D — наружный диаметр;
δ =R —r — ширина кольца; α — центральный угол части кольца (в градусах). |
Площадь части кольца:
|
|
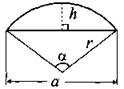
Круговой сегмент
|
r — радиус; α — центральный угол (в градусах);
a — длина хорды; h — высота. |
|
|
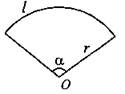
Круговой сектор
|
r — радиус; α — центральный угол (в градусах);
|
|
Инструкция по выполнению работы1
Общее время экзамена — 235 минут. Всего в работе 26 заданий, из которых 20 заданий базового уровня (часть 1) и 6 заданий повышенного уровня (часть 2). Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика».
Модуль «Алгебра» содержит 11 заданий: в части 1—8 заданий с кратким ответом, выбором ответа и установлением соответствия; в части 2—3 задания с полным решением. Модуль «Геометрия» содержит 8 заданий: в части 1—5 заданий с кратким ответом, в части 2—3 задания с полным решением. Модуль «Реальная математика» содержит 7 заданий: все задания — в части 1, с кратким ответом и выбором ответа.
Сначала выполняйте задания части 1. Начать советуем с того модуля, задания которого вызывают у Вас меньше затруднений, затем переходите к другим модулям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Все необходимые вычисления, преобразования и т.д. выполняйте в черновике. Если задание содержит рисунок, то на нём можно выполнять необходимые Вам построения. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться при оценивании работы. Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
При выполнении заданий с выбором ответа обведите номер выбранного ответа в экзаменационной работе. Если Вы обвели не тот номер, то зачеркните обведённый номер крестиком и затем обведите номер нового ответа. Если варианты ответа к заданию не приводятся, полученный ответ записывается в отведённом для этого месте. В случае записи неверного ответа зачеркните его и запишите рядом новый. Если в задании требуется установить соответствие между некоторыми объектами, впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
Решения заданий части 2 и ответы к ним записываются на отдельном листе. Текст задания можно не переписывать, необходимо лишь указать его номер.
Баллы, полученные Вами за верно выполненные задания, суммируются. Для успешного прохождения итоговой аттестации необходимо набрать в сумме не менее 8 баллов, из них не менее 3 баллов по модулю «Алгебра», не менее 2 баллов по модулю «Геометрия» и не менее 2 баллов по модулю «Реальная математика».
Желаем успеха!
1 Разработана специалистами ФИЛИ (www.fipi.rn).