Математика 9 класс подготовка к ГИА
Решения задач из сборника - Сборник задач
60. Умножим числитель и знаменатель каждой дроби на число, сопряжённое знаменателю.
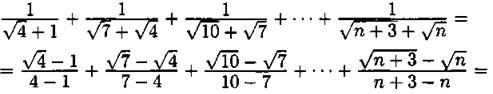
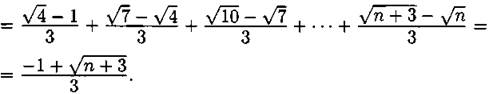
Ответ: ![]()
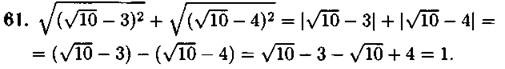
Ответ: 1.
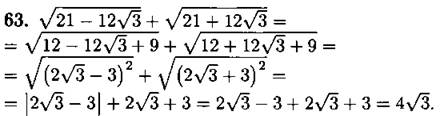
Ответ: 4√3.
![]()
Ответ: n(n + 1)(m — 1).
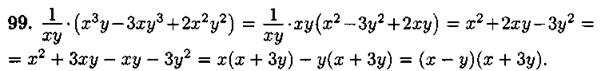
Ответ: (х — у)(х + 3у).
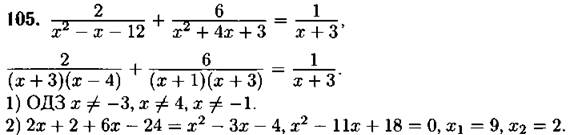
Оба корня принадлежат ОДЗ.
Ответ: 9, 2.
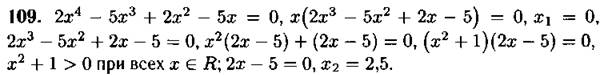
Ответ: 0; 2,5.
137. Представим данное уравнение в виде ![]() Определим знак дискриминанта:
Определим знак дискриминанта:
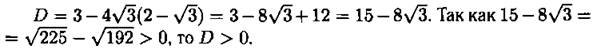
Уравнение ![]() имеет два различных действительных корня.
имеет два различных действительных корня.
Ответ: 2.
![]()
Прибавим к первому уравнению системы второе, умноженное на 2:
![]()
Решение исходной системы свелось к решению двух систем уравнений:
![]()
Решая каждую из этих систем способом подстановки, получим x1 = 1, y1 = 1, x2 = -1, y2 = -1.
Ответ: (1; 1), (—1; —1).
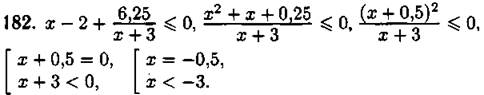
Ответ: (—∞;-3) U {-0,5}.
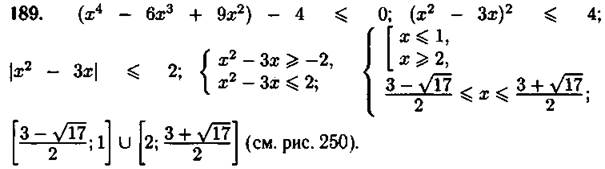
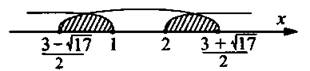
Рис. 250
Ответ: 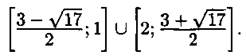
194. Выражение имеет смысл при ж, удовлетворяющих следующим условиям:
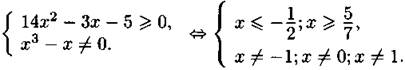
Ответ: ![]()
201. Выражение ![]() имеет смысл при x, удовлетворяющих следующим условиям:
имеет смысл при x, удовлетворяющих следующим условиям:
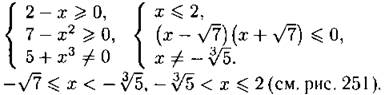

Рис. 250
Ответ: ![]()
241. Данное выражение определено, когда выполняется следующая система:
![]()
Получаем ![]()
Ответ: ![]()
242. Данное выражение определено, когда выполняется следующая система:
![]()
Получаем ![]()
Ответ: ![]()
249. По условию аn = 8n, аn ≤ 200, 8n ≤ 200, n ≤ 25.
Найдём сумму 25 натуральных чисел, кратных 8:
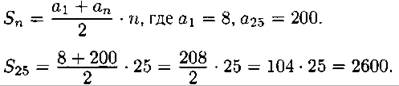
Ответ: 2600.
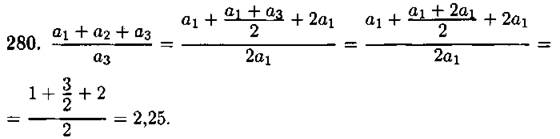
Ответ: 2,25.
281. По условию задачи а8 = 3а6. Тогда ![]() d = a8 — а7 = a6. Так как, с другой стороны, a6 = a1 + 5d, то получим d = a1 + 5d, a1 = —4d.
d = a8 — а7 = a6. Так как, с другой стороны, a6 = a1 + 5d, то получим d = a1 + 5d, a1 = —4d.
Итак, ![]()
Ответ: 0.
285. По условию имеем арифметическую прогрессию an = 4n—3, a1 = 1, d = 4.
Составим новую арифметическую прогрессию из членов прогрессии аn с чётными номерами. Для новой прогрессии получим b1 = а2 = 5, db = 8. Сумма членов исходной прогрессии с чётными номерами, не превосходящими 50, равна сумме первых 25 членов полученной прогрессии.
![]()
Ответ: 2525.
291. Тридцать первых членов с чётными номерами прогрессии аn составляют арифметическую прогрессию bn, такую, что b1 = а2, b2 = а4, ..., b30 = a60. Найдём а2 и a60.
![]()
Переформулируем задачу: найти сумму тридцати членов арифметической прогрессии, если b1 = -64, b30 = 168.
Получаем ![]()
Ответ: 1560.
340. у = |ах + b| + с, а > 0.
Из рисунка видно, что график функции у = |ах + b| опущен на 2 единицы вниз, значит, с = —2. Пусть tgα — угол наклона прямой к положительному направлению оси Ох. Тогда a = tgα = 6/2 = 3 (по условию a > 0). Если х > —2, то у = ах + (b + с). Так как у(0) = 4, то b + с = 4; b = 6.
Ответ: а = 3; b = 6; с = -2.
355. у = х3 — х2 — 4х + 4.
1) С осью Ох
![]()
х3-х2 — 4х + 4 = 0, х2(а: — 1) — 4(ж — 1) — 0, (х — 1)(х2 -4) = 0;ж-1 = 0, Х\ = 1; х2 — 4 = 0, Х2 = 2, хз = —2.
(1;0), (2;0), (—2;0) — координаты точек пересечения графика функции у = х3 — х2 — 4х + 4 с осью Ох.
2) С осью Оу
(0; 4) — координаты точки пересечения графика функции у — х3 — х2 — 4х + 4 с осью Оу.
Ответ: (—2; 0), (1; 0), (2; 0), (0; 4).
415. Пусть скорость первого велосипедиста х км/ч, а второго — у км/ч.
1) первый до встречи прошёл 7,5x км, а второй — 4у км. Составим первое уравнение: 7,5х + 4у = 325;
2) первый до встречи прошёл 5х км, а второй — 7у км. Составим второе уравнение: 5х + 7у = 325.
Получим систему уравнений ![]()
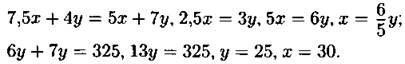
Ответ: 30; 25.
421. Пусть х км/ч — скорость третьего катера, а t ч — время, за которое третий катер догонит второй. Расстояние, которое проплыл второй катер до встречи с третьим, равно 40 ∙ (t + 1) км, а третий катер проплыл xt км. К моменту встречи второго катера с первым второй катер проплыл (2t + 1) ∙ 40 км, а первый катер — (2t + 2) ∙ 30 км.
По условию xt = 40 ∙ (t + 1) и (2t + 1) ∙ 40 = (2t + 2) 30.
Решим систему уравнений:
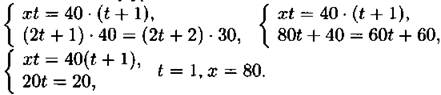
Скорость третьего катера равна 80 км/ч.
Ответ: 80.
442. ![]() было пройдено за изначально намеченное время со скоростью ж км/ч. С увеличенной скоростью (х +10) км/ч было пройдено 420 - 240 = 180 км.
было пройдено за изначально намеченное время со скоростью ж км/ч. С увеличенной скоростью (х +10) км/ч было пройдено 420 - 240 = 180 км.
Планируемое время ![]() больше реального времени
больше реального времени ![]() Составляем уравнение:
Составляем уравнение: ![]() Умножим обе части на 4x2+ 40.
Умножим обе части на 4x2+ 40.
![]()
По теореме, обратной теореме Виета, x1 = —90, x2 = 80.
По смыслу задачи ж = 80 км/ч — исходная скорость. Тогда общее время движения 420 : 80 = 5,25 ч.
Ответ: 5,25.
519. Пусть x — количество стекла первого сорта, у — количество стекла второго сорта, которые надо взять, чтобы получить стекло, пропускающее 60% света. Из условия задачи имеем
![]()
Ответ: 4:3.
532. Введём обозначение ![]() Учитывая, что старший коэффициент квадратного трёхчлена f(x) положителен, можно сделать вывод, что число 3 находится между корнями уравнения f(x) = 0 тогда и только тогда, когда f(3) < 0.
Учитывая, что старший коэффициент квадратного трёхчлена f(x) положителен, можно сделать вывод, что число 3 находится между корнями уравнения f(x) = 0 тогда и только тогда, когда f(3) < 0.
Решим неравенство ![]()
![]()
Ответ: k ∈ (—5; -1).
541. Среднее арифметическое девяти чисел равно 17, значит, сумма этих девяти чисел равна 17 ∙ 9 = 153.
Среднее арифметическое других одиннадцати чисел равно 7, значит, сумма этих одиннадцати чисел равна 7 ∙ 11 = 77.
Тогда сумма всех двадцати чисел равна 153 + 77 = 230, а их среднее арифметическое равно 230 : 20 = 11,5.
Ответ: 11,5.
611. Указанное неравенство не имеет решений, если дискриминант D квадратного уравнения x2 — (6а + 2)x + 9а + 3 = 0 меньше нуля. Вычислим ![]() и решим неравенство 9а2 — 3а — 2 < 0. Для этого решим уравнение 9а2 — 3а — 2 = 0. Корни его а1 = —1/3, а2 = 2/3, а решение неравенства
и решим неравенство 9а2 — 3а — 2 < 0. Для этого решим уравнение 9а2 — 3а — 2 = 0. Корни его а1 = —1/3, а2 = 2/3, а решение неравенства ![]()
Ответ: ![]()
614. Неравенство ах2 + (а - 6)х + а ≥ 0 не имеет решений при отрицательных а, если дискриминант уравнения ах2 + (а — 6)х + а = 0 D = (а — 6)2 — 4а ∙ а < 0. Получаем
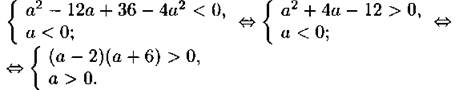
Решая методом интервалов (см. рис. 252), получим а < —6.

Рис. 252
Ответ: а < -6.
620. Построим окружность с центром в точке E(6; 4) радиусом 4 и проведём диаметры BF и АС, параллельные осям координат (см. рис. 253).
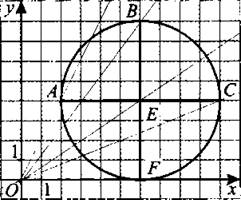
Рис. 253
По рисунку видно, что прямая у = kх имеет ровно одну общую точку с диаметрами АС и BF в трёх случаях.
1. Угловой коэффициент прямой у = kх больше либо равен угловому коэффициенту прямой у = 0 и меньше углового коэффициента прямой ОС.
Найдём угловой коэффициент прямой ОС, как прямой, проходящей через точку C(10; 4): 4 = 10k, k = 2/5.
Угловой коэффициент прямой у = 0 равен 0. Получаем: 0 ≤ k ≤ 2/5.
2. Условию задачи удовлетворяет прямая у — кх, проходящая через центр окружности точку E(6; 4). Найдём угловой коэффициент прямой ОЕ: 4 = 6k, k = 2/3.
3. Угловой коэффициент прямой у = kх больше углового коэффициента прямой ОВ, но меньше либо равен угловому коэффициенту прямой ОА.
Найдём угловой коэффициент прямой ОВ, как прямой, проходящей через точку B(6; 8): 8 = 6k, k = 4/3.
Найдём угловой коэффициент прямой ОА, как прямой, проходящей через точку A(2; 4): 4 = 2k, k = 2.
Получаем 4/3 < k ≤ 2.
Ответ: ![]()
626. Заметим, что ∠AKC = 90° как вписанный угол, опирающийся на диаметр окружности. Тогда середина отрезка ВС — точка D — является центром описанной окружности прямоугольного треугольника ВКС (см. рис. 254).
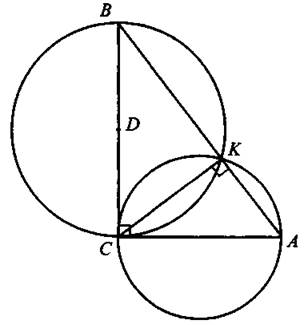
Рис. 254
Так как высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, то ![]() то есть
то есть ![]() При этом
При этом ![]() и, значит,
и, значит, ![]() Тогда
Тогда ![]()
Ответ: 15,6.
636. Так как ![]() то
то ![]() (см. рис. 255). Тогда
(см. рис. 255). Тогда 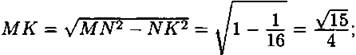
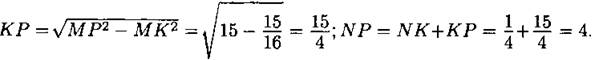
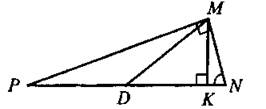
Рис. 255
Так как MN2 + МР2 = NP2, то треугольник MNP — прямоугольный по теореме, обратной теореме Пифагора. Следовательно, ![]()
Ответ: 2.
643. Пусть АВ = ВС = х, ВВ = у, AD = 24, AС = 30 (см. рис. 256).
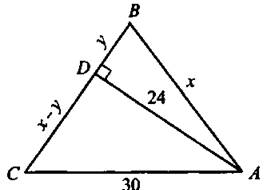
Рис. 256
Используя теорему Пифагора для треугольников ABD и ADC, получим систему уравнений 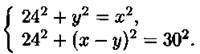
Эта система имеет единственное решение х = 25, у = 7, удовлетворяющее условиям х > 0, у > 0.
Ответ: 25.
645. Пусть АВ = х, АС = у (см. рис. 257). Тогда из условия задачи следует совокупность систем уравнений:
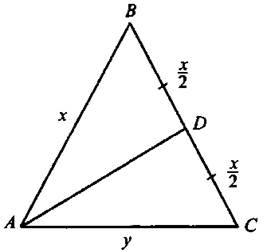
Рис. 257
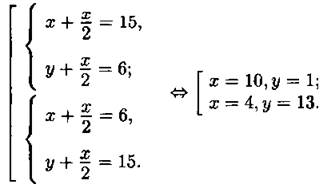
Так как во втором случае не выполняется одно из неравенств треугольника 2х > у, то АВ = 10.
Ответ: 10.
647. Пусть АВ = KL = CD = x, AM = МВ и CN = ND (см. рис. 258). Тогда ∠EAD = ∠ВЕА как накрест лежащие. Кроме того, АЕ — биссектриса ∠BAD. Следовательно, ∠ВАЕ = ∠BEА, и ∆АВЕ — равнобедренный.
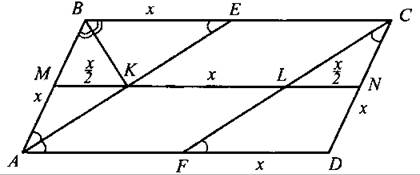
Рис. 258
Так как ВК — биссектриса, проведённая к основанию равнобедренного треугольника АВЕ, то ВК — медиана этого треугольника. Таким образом, МК — средняя линия ∆АВЕ, то есть ![]() и МК || ВС. Аналогично доказывается то, что LN = x/2 и LN || AD.
и МК || ВС. Аналогично доказывается то, что LN = x/2 и LN || AD.
AECF — параллелограмм, так как AF || ЕС и AF = ЕС = ВС - х. Тогда AKLF — также параллелограмм, так как АК || FL и АК = FL. Следовательно, KL || AD и точки М, К, L и N лежат на одной прямой, причём ![]() Таким образом,
Таким образом, ![]()
Ответ: 2.
659. Возможны два случая:
1) Центр описанной окружности находится внутри трапеции (см. рис. 259).
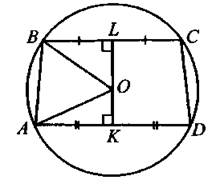
Рис. 259
Тогда 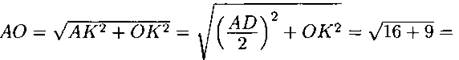
![]() — радиус описанной окружности;
— радиус описанной окружности; ![]()
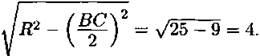 Высота трапеции LX = LO + OK= 4 + 3 = 7.
Высота трапеции LX = LO + OK= 4 + 3 = 7.
2) Центр описанной окружности находится вне трапеции (см. рис. 260).
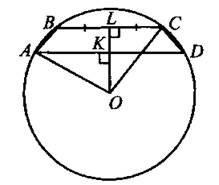
Рис. 260
Тогда 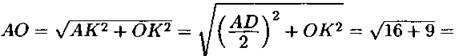
![]() — радиус описанной окружности;
— радиус описанной окружности; ![]()
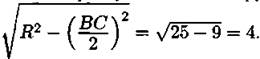 Высота трапеции LX = LO — ОK= 4 - 3= 1.
Высота трапеции LX = LO — ОK= 4 - 3= 1.
Ответ: 1; 7.
662. Так как трапеция равнобочная, то вокруг неё можно описать окружность (см. рис. 261). Тогда ∠ВАС = ∠BDC как вписанные углы, опирающиеся на одну и ту же дугу. Следовательно, ∆AOD — равнобедренный (∠OAD = ∠ODA, так как углы при основании равнобочной трапеции равны и ∠ВАС = ∠BDC) и, так как он прямоугольный, то ∠OAD = 45°. Но треугольник АОК также прямоугольный с острым углом в 45°, следовательно, он равнобедренный, и АК = ОК.
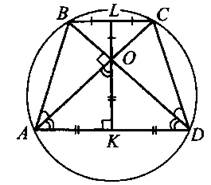
Рис. 261
Аналогично можно доказать, что OL = BL. Значит, ![]() где MN — средняя линия трапеции.
где MN — средняя линия трапеции.
Ответ: 4.
670. Так как ![]() (см. рис. 262). Из треугольника OMD получим
(см. рис. 262). Из треугольника OMD получим ![]() Из треугольника O1MD получим
Из треугольника O1MD получим ![]()
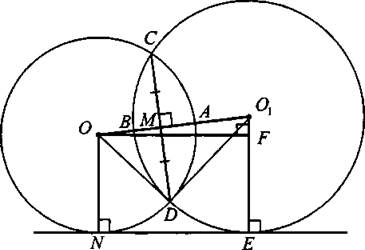
Рис. 262
Тогда ОО1 = ОМ + О1М = 5 + 16 = 21; O1F = О1Е - ON = 20 — 13 = 7. Из треугольника O1OF получим ![]()
![]()
Ответ: 14√2.