Математика 5 класс - Поурочные разработки
Деление с остатком - Деление с остатком - Делимость чисел
Цель: закрепить умение решать примеры на все арифметические действия, сформировать умение делить с остатком.
Ход урока
I. Организационный момент.
II. Устная работа.
Вычислите:
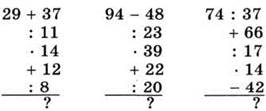
III. Актуализация знаний.
1. Найдите значение выражения 308 · 46 : 56 + 48 · 501 : 72 - 439.
На доске выполняется решение примера по действиям.
2. Выполните примеры на деление: 250 908 : 618; 81 606 : 201; 65 049 : 78. При решении последнего примера возникает проблема, которую учитель решает вместе с учащимися. Учащиеся самостоятельно должны сделать вывод: при делении числа 65 049 на число 78 получается остаток 75. Далее вспоминаем из курса начальной школы понятия: 65 049 — делимое; 78 — делитель; 833 — неполное частное; 75 — остаток.
1). Мог ли остаток при выполнении деления получиться 80? 45? 100? Сделать вывод: остаток всегда меньше делителя.
2). Какие остатки могут получиться при делении числа: на 3; на 8; на 5; на 10?
IV. Формирование умений и навыков.
1. Совместная работа с классом.
Мы знаем, что не всегда одно натуральное число делится на другое. Но всегда можно выполнить деление с остатком. Что значит разделить с остатком? Чтобы ответить на этот вопрос, решим задачу.
Шофер городского автобуса приступил к работе в 7 ч, а обеденный перерыв у него начинается в 12 ч. Один рейс автобуса длится 48 мин. Сколько рейсов успеет сделать шофер до обеда? Сколько минут у него останется для осмотра автобуса?
Рассуждаем так: всего до обеда шофер проработает 5 ч, т. е. 300 мин. 300 : 48 = 6 (ост. 12), значит, шофер успеет сделать до обеда 6 рейсов и 12 мин у него останется на осмотр автобуса. Если сложить время, потраченное на 6 рейсов (6 · 48 мин), и время, потраченное на осмотр автобуса (12 мин), то получится все рабочее время до обеда, т. е. 300 мин. 300 = 48 · 6 + 12.
Вообще, при делении с остатком верно свойство: делимое равно произведению делителя и частного, сложенному с остатком. Следовательно, разделить с остатком число а на число b — значит найти два таких числа с и d (частное и остаток), что а = b · с + d, где d < b.
2. Закрепление полученных знаний.
1). Назовите остаток при делении:
а) 346 на 10; б) 346 на 100; в) 47 на 5; г) 31 на 5; д) 100 на 9.
2). Выполните деление с остатком и сделайте проверку: 451 : 3; 1852 : 33; 14 090 : 134; 27 549 : 25.
3). Самостоятельная работа по вариантам с последующей проверкой и обсуждением.
Вариант 1. У, № 595 (а), 596 (а), 597 (а), 598 (а), 599 (а).
Вариант 2. У, № 595 (б), 596 (б), 597 (б), 598 (б), 599 (б).
V. Итоги урока.
1. Что значит разделить с остатком одно число на другое?
2. Каким равенством связаны делимое, делитель, частное и остаток?
VI. Домашнее задание.
У, п. 6.5, № 601, 602, выполнить деление с остатком и сделать проверку: 7431 : 28; 34 217 : 37; 6829 : 55; 12 437 : 113.