Математика 5 класс - Поурочные разработки
Приведение дробей к общему знаменателю - Приведение дробей к общему знаменателю - Дроби
Цель: развивать умение приводить дроби к общему знаменателю, рассмотрев разные приемы нахождения общего знаменателя.
Ход урока
I . Организационный момент.
II. Устная работа.
1. При каких значениях а дробь a/9 будет меньше дроби 8/9?
2. При каких значениях а дробь a/18 будет больше дроби 7/18, но меньше дроби 13/18?
3. РТ, часть 1, № 112, с. 42.
4. Расположите дроби в порядке возрастания:
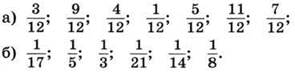
III. Актуализация знаний.
1. Расположите дроби 5/12; 4/9; 7/18 в порядке возрастания. Как это можно сделать? Приведите дроби к одному знаменателю.
2. Приведите дроби к новому знаменателю: ![]()
![]() Можно ли дробь 2/3 привести к знаменателю 9; 12; 14; 22; 36? И т. д. (новый знаменатель должен быть кратен 3).
Можно ли дробь 2/3 привести к знаменателю 9; 12; 14; 22; 36? И т. д. (новый знаменатель должен быть кратен 3).
IV. Изучение нового материала.
К каким новым знаменателям можно привести дроби 3/4 и 2/5?
3/4 к 8, 12, 16, 20, 24, ..., 2/5 к 10, 15, 20, 25, ... . Общим знаменателем является 20, это число, кратное 4 и 5: ![]()
Вывод. Привести дроби к общему знаменателю — значит найти равные им дроби с одинаковыми знаменателями. Обычно дроби приводят к наименьшему общему знаменателю, который равен их наименьшему общему кратному.
V. Формирование умений и навыков.
1. Нахождение наименьшего общего кратного двух чисел. ДМ, 0-27, № 1, 2.
2. Приведение дробей к общему знаменателю. Работа с текстом п. 8.4 учебника.
1). Рассмотреть пример 1, выполнить № 808.
2). Рассмотреть пример 2, выполнить № 809.
3). Рассмотреть пример 3, выполнить № 810.
4). Выполнить № 813.
VI. Итоги урока.
1. Что значит привести дроби к общему знаменателю?
2. Чему равен наименьший общий знаменатель двух несократимых дробей?
VII. Домашнее задание.
У, п. 8.4, № 806, 811, 812.