РЕШЕНИЕ УРАВНЕНИЙ

Оборудование: ксерокопии текстов каждого варианта.

Ход урока

I. Проверка домашнего задания.

Выполнить тест.

Вариант I

1. Вычислите: 3,34 + 28,7.

1) 32,04; 2) 31,41; 3) 31,04; 4) 62,1.

2. Вычислите: 0,34  0,8.

1) 2,72; 2) 0,272; 3) 27,2; 4) 0,0272.

3. Вычислите: 20,4 : 0,8.

1) 25,5; 2) 2,55; 3) 0,255; 4) 255

4. Округлите 0,6539 до сотых.

1) 0,7; 2) 0,65; 3) 0,66; 4) 0,654.

5. Расположите в порядке убывания числа 3,78; 3,784; 3,7801.

1) 3,7801; 3,78; 3,784; 2) 3,784; 3,78; 3,7801;

3) 3,784; 3,7801; 3,78; 4) 3,78; 3,7801; 3,784.

6. Выразите в метрах 0,002 км.

1) 20 м; 2) 200 м; 3) 2 м; 4) 2000 м.

7. Найдите площадь квадрата, сторона которого равна 1,1 дм.

1) 4,4 дм2; 2) 1,21 дм2; 3) 2,2 дм2; 4) 121 дм2.

8. Из чисел 1; ; 1,05; выберите наименьшее.

1) 1; 2) ; 3) 1,05; 4) .

Фамилия, имя____________________________ класс________
№ задания	1	2	3	4	5	6	7	8
№ ответа

Вариант II

1. Вычислите: 6,35 – 3,5.

1) 2,85; 2) 3,3; 3) 6; 4) 3,85.

2. Вычислите: 0,7  0,26.

1) 0,182; 2) 0,0182; 3) 1,82; 4) 18,2.

3. Представьте в виде десятичной дроби .

1) 0,725; 2) 0,28; 3) 0,028; 4) 2,8

4. Округлите 0,2518 до десятых.

1) 0,25; 2) 0,2; 3) 0,3; 4) 0,251.

5. Расположите в порядке возрастания числа 1,4302; 1,43; 1,437.

1) 1,437; 1,4302; 1,43; 2) 1,43; 1,4302; 1,437;

3) 1,437; 1,43; 1,4302; 4) 1,4302; 1,43; 1,437.

6. Выразите в тоннах 16 кг.

1) 0,16 т; 2) 0,00016 т; 3) 0,0016 т; 4) 0,016 т.

7. Найдите периметр квадрата, сторона которого равна 1,3 дм.

1) 16,9 дм; 2) 2,6 дм; 3) 5,2 дм; 4) 1,3 дм.

8. Из чисел 0,98; ; 1; выберите наибольшее.

1) 0,98; 2) ; 3) 1; 4) .

Фамилия, имя____________________________ класс________
№ задания	1	2	3	4	5	6	7	8
№ ответа

II. Устные упражнения.

1. Решите уравнения. Заполните таблицу буквами, учитывая найденные ответы.

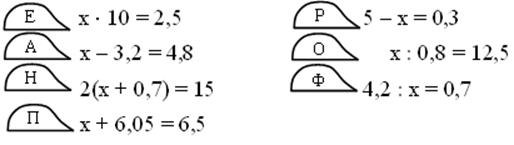
0,45	8	4,7	6	0,25	6,8	10

Что означает полученное слово?

(Ответ: Парфенон, храм Афины Парфенос на Акрополе в Афинах, памятник древнегреческой высокой классики, построен в 432 г. до н. э.)

2. Найдите корни уравнения:

х  1 = 0 0  х = 1 х – х = 0 х – х = 1

х – 10 = 10 х + 10 = 10 0  х = 0 0 + х = 10

х – 10 = 0 х : 10 = 10 0 : х = 1.

III. Тренировочные упражнения:

1. Решить уравнение:

а) (х – 5,6) : 12 = 3,7 б) (х + 2,1)  4 = 15,2 (2-я способами)

в) 3,4 – 9х = 1,6 г) 8,1 : х – 0,7 = 3

д) s : 2,3 = 4,6 е) 9,88 : (6,7 – х) = 2,6

ж) 6,7  (7,9 – у) = 28,81 з) 9,14z – (3,78z + 2,87z) = 12,45.

2. Решить самостоятельно:

а) 41 – 7,08у = 23,3 б) 4,6х + 3,8х –1,6 = 0,5

IV. Итог урока.

1. Можно привести высказывание Д. Чосера:

«Посредством уравнений, теорем

Он уйму всяких разрешил проблем:

И засуху предсказывал, и ливни.

Поистине его познанья дивны».

2. Решить уравнения:

а) 0,3х + 2,4 х = 270; б) 0,2  (4х + х) = 12; в) 2х + х + 0,6 = 4,2.

Используя найденные ответы, узнайте имена клоунов, если известно, что у Бима корень уравнения совпадает с ответом примера 40  1,25  0,8  2,5 =…, а у Бома корень уравнения наименьший. Третьего клоуна зовут Бум.

V. Домашнее задание: № 1817, 1828, 1876.