Отношения - ОТНОШЕНИЯ И ПРОПОРЦИИ - ОБЫКНОВЕННЫЕ ДРОБИ

Пропорция. Основное свойство пропорции. Решение задач с помощью пропорции. Понятия о прямой и обратной пропорциональностях величин. Задачи на пропорции. Масштаб. Формулы длины окружности и площади круга. Шар.

Основная цель — сформировать понятия пропорции, прямой и обратной пропорциональностей величин.

Необходимо, чтобы учащиеся усвоили основное свойство пропорции, так как оно находит применение на уроках математики, химии, физики. В частности, достаточное внимание должно быть уделено решению с помощью пропорции задач на проценты.

Понятия о прямой и обратной пропорциональностях величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув при этом практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач.

В данной теме даются представления о длине окружности и площади круга. Соответствующие формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром.

ОТНОШЕНИЯ (3 ч)

Урок 75. Отношения

Цель: ввести понятие отношения и процентного отношения двух чисел; определить, что показывает отношение; показать, где применяется отношение двух чисел; формировать вычислительные навыки.

Информация для учителя

Обратить внимание учащихся, что при нахождении отношения двух чисел очень важно понимать, какое число из двух данных чисел берется делимым, а какое - делителем.

Ход урока

I. Организационный момент

— Сегодня наш девиз: «Математика — это гимнастика ума».

— Как вы его понимаете?

— Что в математике позволяет тренировать наш ум?

II. Анализ контрольной работы

1. Познакомить учащихся с результатами контрольной работы.

2. Решить задания, где допущено наибольшее количество ошибок, задания, вызвавшие затруднения у учащихся.

III. Устный счет

1. Найдите 20% от чисел: 40; 200; 18; 1000; 3; 120; 0,6; 0,08..

2. Найдите значение выражений: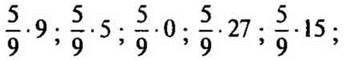

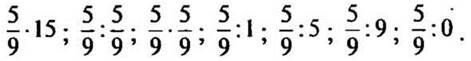
— Значение последнего выражения найти не можем, так как делить на 0 нельзя.

3. Периметр прямоугольника равен 48 см, длина на 4 см больше ширины. Найдите стороны прямоугольника.

IV. Индивидуальная работа

1 карточка

Вычислить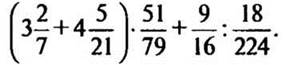

2 карточка

Вычислить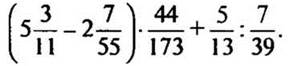

V. Сообщение темы урока

— Сегодня на уроке мы познакомимся с понятием «отношение двух чисел» и узнаем, что оно показывает.

VI. Изучение нового материала

1. Алгоритм работы в парах (можно распечатать каждому на парту или написать на доске; можно работать под руководством учителя).

1. Прочитайте задачу 1 п. 20, стр. 117 (один ученик читает, другой слушает).

2. Разберите решение этой задачи.

3. Запишите решение в тетрадь. Если есть вопросы, обсудите их с партнером по парте или проконсультируйтесь у учителя.

4. Прочитайте 1 предложение, выделенное жирным шрифтом. Что это такое? (Определение.)

5. Запишите в тетрадь определение отношения двух чисел.

6. Выучите это определение

7. Сдайте друг другу определение, проверяя по учебнику. Если есть вопросы, выясните их с помощью учителя или партнера. Если вопросов нет, приступайте к индивидуальной работе.

2. Индивидуальная работа.

Выполните № 722 стр. 118 (если класс слабый, выполнить только а—г).

8. Сверьте ответы, придите к одному решению (в паре).

9. Исправьте ошибки.

(Ответы: )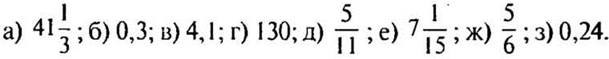

3. Фронтальная работа.

Проверка выполненных решений (проговаривание ответов). Если остается один ученик без пары, то работает с учителем, записывает решение на обратной стороне доски. Тогда возможен вариант сверки ответов с решением на доске.

Отношение — содержание, пропорция, вывод сравнения двух чисел, вычитанием (отношение арифметическое), делением (отношение геометрическое). (Из толкового словаря В. И. Даля.)

1) Давайте вернемся к рассмотренной вами задаче.

— Прочитайте ответ. Сколько вариантов ответа? (Два: один в виде обыкновенной дроби, другой — в виде десятичной, которая переведена в проценты.)

Отношение может быть выражено в процентах, тогда его называют процентным отношением.

— Что оно показывает? (Сколько процентов одно число составляет от другого.)

— Как найти процентное отношение? (Надо найти отношение и потом выразить его в процентах.)

2) Решите задачи:

(Записаны на доске или на карточках.)

1. Скорость первого пешехода равна 6 км/ч, скорость второго — 5 км/ч.

Во сколько раз скорость первого пешехода больше скорости второго пешехода?

Решение:

6 : 5 = 1,2 (раза)

(Ответ: в 1,2 раза.)

2. Первый турист прошел 12 км, второй турист — 18 км.

Какую часть пути второго туриста составляет путь первого?

Решение:

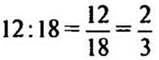(части)

— Чтобы ответить на вопросы задач, что мы находили? (Частное.)

— Как по-другому называется частное двух чисел? (Отношением этих чисел.)

— Что показывает отношение двух чисел? (Во сколько раз первое число больше второго, или какую часть первое число составляет от второго.)

— Найдите отношения: 5 к 12; 5 к 2; 8 к 13; 13 к 8.

(Ответы: )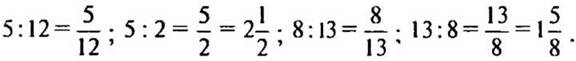

— Как по записи понять, что показывают данные отношения?

— Отношение, большее единицы, показывает, во сколько раз одно число больше (меньше) другого.

— Отношение, меньшее единицы, показывает, какую часть (дробь) одно число составляет от другого.

— Отвечая на вопросы задач, будьте очень внимательны.

— При нахождении отношения двух чисел, важно понимать, какое число из двух данных будет делимым, какое — делителем.

VII. Закрепление изученного материала

1. № 723 стр. 118 (один учащийся решает на обратной стороне доски, остальные в тетрадях).

— Прочитайте задачу.

— Что надо знать, чтобы узнать, какую часть всей проволоки составляет первый кусок? (Нужно знать длину всей проволоки.)

— Как узнать длину всей проволоки? (Сложить ее части.)

— Как узнать, какую часть один кусок составляет от всей проволоки? (Найти отношение длины этого куска к длине всей проволоки.)

— Как узнать, какую часть длина первого куска составляет от длины второго куска? (Найти отношение длины первого куска к длине второго куска.)

Решение:

1) 9 + 14,4 = 23,4 (м) - длина всей проволоки.

2) 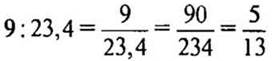(частей) — всей проволоки составляет первый кусок.

3) 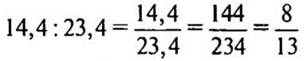(частей) - всей проволоки составляет второй кусок.

4) 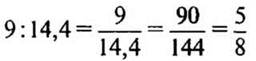(частей) - составляет первый кусок от длины второго куска.

(Ответы: )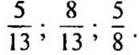

2. № 732 стр. 119 (устно).

— Почему вы так считаете?

Ответы:

а) Какую часть молоко из первого бидона составляет от молока из второго бидона.

б) Какую часть молоко из первого бидона составляет от молока из третьего бидона.

в) Какую часть молоко из второго бидона составляет от молока из третьего бидона.

г) Какую часть все молоко из первого и второго бидонов составляет от молока из третьего бидона.

— Какие еще отношения можно составить?

— Что они показывают?

0,3 к 0,1;

0,1 к (0,1 + 0,6); 0,3 к (0,1 + 0,6); 0,6 к (0,1 + 0,6);

0,3 к (0,1 + 0,6 + 0,3); 0,1 к (0,1 + 0,6 + 0,3); 0,6 к (0,1 + 0,6 + 0,3) и т. д.

4. Самостоятельная работа.

Для мальчиков. Какую часть вашего класса составляют девочки? Ответ выразите в процентах.

Для девочек. Какую часть вашего класса составляют мальчики? Ответ выразите в процентах.

VIII. Физкультминутка

IX. Повторение изученного материала

1. № 743 стр. 121.

— Во сколько раз числитель одной дроби больше числителя другой дроби? (В 5 раз.)

— Значит, знаменатель надо увеличить тоже в 5 раз.

— Определите, на сколько нужно увеличить знаменатель дроби.

Решение:

на 8: 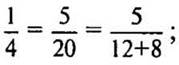на 11: 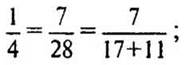увеличивать не надо: 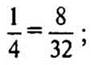на 5: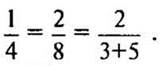

(Ответ: 8; 11; не надо увеличивать; 5.)

2. Задание на внимание. Работа в парах.

№ 746 стр. 121.

Вариант I — первая таблица.

Вариант II — вторая таблица.

X. Подведение итогов урока

— Что называют отношением двух чисел?

— Что показывает отношение двух чисел?

— Что такое процентное отношение двух чисел?

Домашнее задание

Учебник, стр. 118 (прочитать текст под рубрикой «Говори правильно»).

Вести словарь математических терминов по теме «Отношения и пропорции».

№ 751, 754 стр. 122; № 759 (а) стр. 123.