Высказывание. Логические операции - МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ УРОКОВ В 8 КЛАССЕ

Планируемые образовательные результаты:

• предметные — представления о разделе математики — алгебре логики, высказывании как ее объекте, об операциях над высказываниями;

• метапредметные — навыки анализа логической структуры высказываний; понимание связи между логическими операциями и логическими связками, между логическими операциями и операциями над множествами;

• личностные — понимание роли фундаментальных знаний как основы современных информационных технологий.

Решаемые учебные задачи:

1) закрепление навыков представления чисел в памяти компьютера;

2) знакомство с понятием высказывания, с простыми и сложными, истинными и ложными высказываниями;

3) знакомство с логическими операциями (И — конъюнкцией, ИЛИ — дизъюнкцией, НЕ — инверсией) и приоритетом их выполнения;

4) отработка умений составления логических выражений, соответствующих сложным высказываниям.

Основные понятия, рассматриваемые на уроке:

• алгебра логики;

• высказывание;

• логическая переменная;

• логическое значение;

• логическая операция;

• конъюнкция;

• дизъюнкция;

• отрицание.

Средства ИКТ, используемые на уроке:

• персональный компьютер (ПК) учителя, мультимедийный проектор, экран;

• ПК учащихся.

Электронное приложение к учебнику:

• презентация “Элементы алгебры логики”.

Единая коллекция цифровых образовательных ресурсов:

1) тренировочный тест “Двоичная система счисления и представление чисел в памяти компьютера” (119342);

2) демонстрация к лекции “Основные понятия математической логики” (128630);

3) демонстрация к лекции “Вычисление логических выражений” (128658).

Федеральный центр информационных образовательных ресурсов:

1) информационный модуль “Высказывание. Простые и сложные высказывания. Основные логические операции”;

2) практический модуль “Высказывание. Простые и сложные высказывания. Основные логические операции”.

Особенности изложения содержания темы урока

В начале урока осуществляется:

1) визуальная проверка выполнения заданий в РТ и к параграфу;

2) рассмотрение заданий, вызвавших затруднения при выполнении домашнего задания.

Далее целесообразно в течение 10-12 минут провести небольшую проверочную работу по уже изученному материалу с использованием тренировочного теста “Двоичная система счисления и представление чисел в памяти компьютера”.

Новый материал излагается в сопровождении презентации “Элементы алгебры логики”, в процессе изложения нового материала выполняются задания № 1—6 к параграфу 1.3; выполняются задания № 78, 80, 81 в РТ.

Далее рекомендуется выборочно выполнить задания практического модуля “Высказывание. Простые и сложные высказывания. Основные логические операции” — можно выводить задания на экран и вызывать “к доске” учеников для их решения.

Домашнее задание

§ 1.3 (пункты 1, 2); задания № 76, 77, 79, 82 в РТ.

Дополнительное задание: работа с информационным модулем ФЦИОР “Высказывание. Простые и сложные высказывания. Основные логические операции”.

Указания, комментарии, ответы и решения

Задания в учебнике

№ 4. См. комментарии к № 77 в РТ.

№ 5

1) Неверно, что сегодня в театре идет опера “Евгений Онегин”.

2) Неверно, что каждый охотник желает знать, где сидит фазан. (Не каждый охотник желает знать, где сидит фазан.)

3) Неверно, что число 1 есть простое число. (Число 1 не является простым числом.)

4) Натуральные числа, оканчивающиеся цифрой 0, являются простыми числами.

5) Число 3 не является делителем числа 198.

6) Коля решил не все задания контрольной работы.

7) Неверно, что во всякой школе некоторые ученики интересуются спортом.

8) Неверно, что некоторые млекопитающие не живут на суше.

Задания в рабочей тетради

№ 77

а) А = “Солнце движется вокруг Земли”;

б) А = “Число 376 четное”, В = “Число 376 трехзначное”; А & В (А ^ В).

в) А = “Новый год мы встретим на даче”, В = “Новый год мы встретим на Красной площади”; А | В (A v В).

г) А = “Земля имеет форму шара”. В = “Земной шар из космоса кажется голубым”; А & В (А ^ В).

д) А = “На уроке математики старшеклассники отвечали на вопросы учителя”, В = “На уроке математики старшеклассники писали самостоятельную работу”; А & В (А ^ В).

е) А = “Зимой мальчики играют в хоккей”, B = “Зимой мальчики играют в футбол”;

№ 78

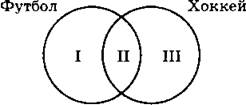
По условию:

I + II + III = 20 000,

I + II = 14 000,

II + III = 16 000.

Отсюда:

II = (I + II) + (II + III) - (I + II + III) = 14 000 + 16 000 - 20 000 = 10 000.

Ответ: 10 000 тысяч страниц.

№ 79

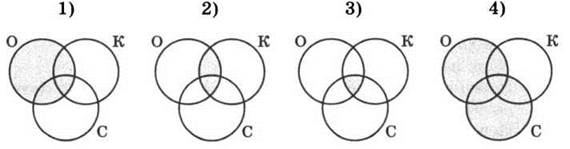
Ответ: 3214.

№ 80

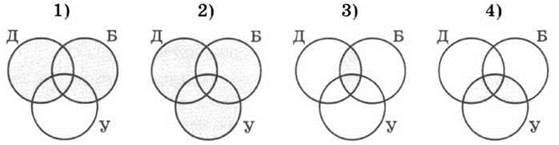
Однозначно нельзя сказать, какое из множеств меньше: 3 или 4. Но каждое из них меньше 1 и 2.

№ 81. Рассуждать можно так: количество сайтов, которые будут найдены по запросу ЧЕРНИКА|МАЛИНА|БРУСНИКА, равно количеству элементов в объединении соответствующих множеств. Для его подсчета можно к количеству элементов множества ЧЕРНИКА (350) прибавить количество элементов множества МАЛИНА без ЧЕРНИКИ (200 - 20) и прибавить количество элементов множества БРУСНИКА без ЧЕРНИКИ и без МАЛИНЫ (500 - 10 - 20 + 5).

Получим: 350 + (200 - 20) + (500 - 10 - 50 + 5) = 975.

№ 82