Информатика - Методическое пособие для 7-9 классов - 2015 год
Построение таблиц истинности для логических выражений - МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ УРОКОВ В 8 КЛАССЕ
Планируемые образовательные результаты:
• предметные — представление о таблице истинности для логического выражения;
• метапредметные — навыки формализации и анализа логической структуры высказываний; способность видеть инвариантную сущность внешне различных объектов;
• личностные — понимание роли фундаментальных знаний как основы современных информационных технологий.
Решаемые учебные задачи:
1) проверка знания основных логических операций;
2) закрепление навыков формализации логических выражений;
3) рассмотрение алгоритма построения таблиц истинности;
4) отработка навыков построения таблиц истинности для логических выражений.
Основные понятия, рассматриваемые на уроке:
• логическая переменная;
• логическое значение;
• логическая операция;
• конъюнкция;
• дизъюнкция;
• отрицание;
• таблица истинности.
Средства ИКТ, используемые на уроке:
• персональный компьютер (ПК) учителя, мультимедийный проектор, экран;
• ПК учащихся.
Электронное приложение к учебнику:
• презентация “Элементы алгебры логики”.
Федеральный центр информационных образовательных ресурсов:
1) информационный модуль “Построение отрицания к простым высказываниям, записанным на русском языке”;
2) практический модуль “Построение отрицания к простым высказываниям, записанным на русском языке”;
3) контрольный модуль “Построение отрицания к простым высказываниям, записанным на русском языке”.
Особенности изложения содержания темы урока
В начале урока осуществляется:
1) визуальная проверка выполнения заданий в РТ;
2) рассмотрение заданий, вызвавших затруднения при выполнении домашнего задания;
3) экспресс-проверка (в течение 5 минут) у учеников знания основных логических операций — соответствующие таблицы истинности ученики записывают на листочках и сдают их учителю.
Далее рекомендуется проработать информационный и практический модули ФЦИОР “Построение отрицания к простым высказываниям, записанным на русском языке”; выполнить № 6, 7 и 11 к параграфу.
Новый материал излагается в сопровождении презентации “Элементы алгебры логики”, в процессе изложения материала выполняется задание № 8 к параграфу 1.3.
Домашнее задание
§ 1.3 (пункт 3); задание № 10 к параграфу; задание № 83 в РТ.
Дополнительное задание: работа с практическим модулем ФЦИОР “Построение отрицания к простым высказываниям, записанным на русском языке”.
Указания, комментарии, ответы и решения
Задания в учебнике
№ 6
6) Ане не нравятся уроки математики или Ане не нравятся уроки химии.
7) Неверно, что Ане нравятся уроки математики и химии.
8) Неверно, что Ане нравятся уроки математики или химии.
9) Неверно, что Ане нравятся уроки математики и не нравятся уроки химии.
№ 7. Так как по запросу сомики&гуппи найдено 0 сайтов, то с помощью кругов Эйлера условие задачи можно представить так:
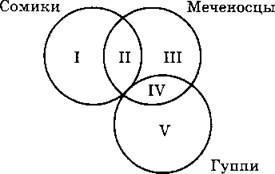
Чтобы найти количество сайтов, соответствующих запросу сомики|меченосцы|гуппи, к количеству элементов множества сомики (250) добавим количество элементов множества меченосцы без сомиков (200 - 20), а также гуппи без меченосцев (500 - 10). Получаем: 250 + 180 + 490 = 920.
№ 8
1)
|
А |
В |
AvB |
B&(AvB) |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
2)
|
А |
В |
|
|
|
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
3)
|
А |
В |
C |
AvBvC |
AvBvC |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
4)
|
А |
В |
С |
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
№ 10. А = 23 = 101112; В = 19 = 100112; С = 26 = 110102.
|
А |
В |
С |
(AvB)&C |
|
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
100102 = 1810.
Ответ: 100102 = 1810.
№ 11. 1) 1; 2) 1; 3) 0; 4) 1; 5) 1; 6) 1; 7) 0; 8) 1; 9) 1; 10) 1.
Задания в рабочей тетради
№ 83
а)
|
А |
В |
А&В |
AvA&B |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
б)
|
А |
В |
AvB |
A&(AvB) |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
в)
|
А |
В |
А&В |
¬А |
¬А&В |
А&Вv¬А&В |
|
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
1 |
г)
|
А |
В |
AvB |
¬А |
¬AvB |
(AvB)&(¬AvB) |
|
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
д)
|
А |
В |
С |
AvBvC |
B&(AvBvC) |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
е)
|
А |
В |
С |
А&В |
A&BvC |
¬(A&BvC) |
|
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
0 |