Преобразование логических выражений - Основы логики

Задание 3.2.1. Заполните пустые ячейки в таблице и проверьте верность логического закона:

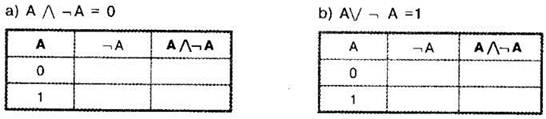
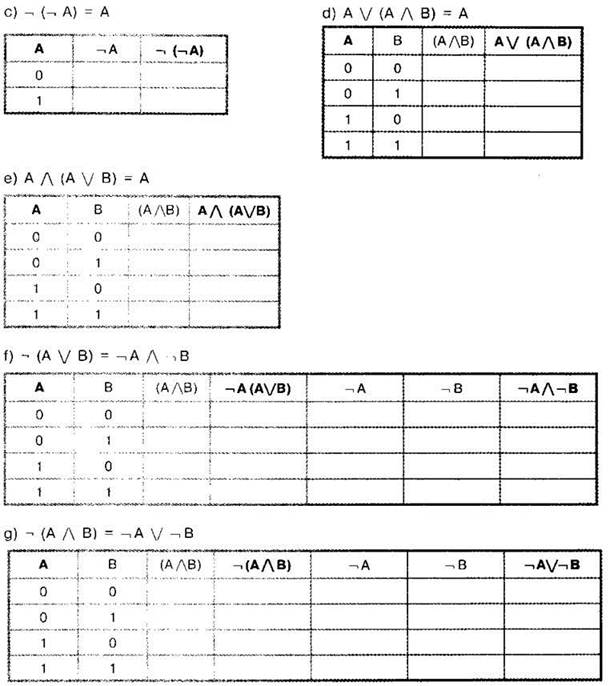
Задание 3.2.2. Запишите выражение, эквивалентное данному, содержащее не более одной операции отрицания. Постарайтесь, чтобы это выражение было как можно более коротким.

Задание 3.2.3. Запишите выражение, эквивалентное данному, не содержащее ни одной операции конъюнкции. Постарайтесь, чтобы это выражение было как можно более коротким.

Задание 3.2.4. Запишите выражение, эквивалентное данному, не содержащее ни одной операции дизъюнкции. Постарайтесь, чтобы это выражение было как можно более коротким.

Задание 3.2.5. Упростите выражение так, чтобы в нём содержалось как можно меньше логических операций и скобок, и постройте его таблицу истинности:

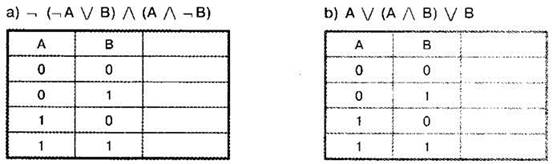
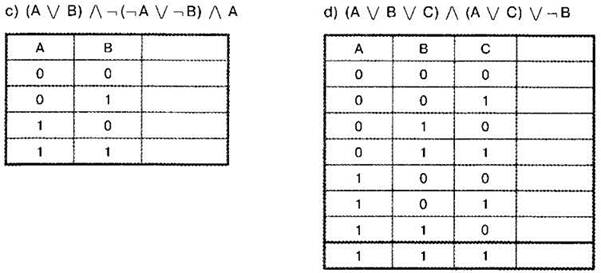
Задание 3.2.6.

a) А, В, С — целые числа, для которых истинно высказывание Укажите наименьшее число С, удовлетворяющее этому условию, если А = 20, В = 30.

Ответ: ________________.

B) Каково наибольшее целое число X, при котором истинно высказывание

Ответ: ________________.

c) Каково наибольшее целое число X, при котором истинно высказывание

Ответ: ________________.

d) А, В, С — целые числа, для которых истинно высказывание Чему равно С, если А = 35, В = 28?

Ответ: ________________.

е) А, В, С — целые числа, для которых истинно высказывание Чему равно С, если А = 12, В = 22?

Ответ: ________________.

Задание 3.2.7.

a) На числовой прямой даны два отрезка: В = [7; 14] и С = [12; 15]. Укажите наибольшую возможную длину такого отрезка А, что формула тождественно истинна (то есть принимает значение 1 при любом значении переменной х).

Ответ: ________________.

B) На числовой прямой даны два отрезка: В = [5; 14] и С = [9; 11]. Укажите наибольшую возможную длину такого отрезка А, что формула тождественно истинна (то есть принимает значение 1 при любом значении переменной х).

Ответ: ________________.

c) На числовой прямой даны два отрезка: В = [12; 15] и С = [12; 25]. Укажите наименьшую возможную длину такого отрезка А, что формула тождественно истинна (то есть принимает значение 1 при любом значении переменной х).

Ответ: ________________.

d) Для какого наименьшего числа А, не равного 1, формула (х кратно 7) V Ш (х кратно 35) V (х кратно А), где А и х — натуральные числа, тождественно истинна (то есть принимает значение 1 при любом значении переменной х)?

Ответ: ________________.

e) Для какого наименьшего числа А, не равного 1, формула ¬((х кратно 3) Λ (х кратно 33)) V (х кратно А), где А и х — натуральные числа, тождественно истинна (то есть принимает значение 1 при любом значении переменной х)?

Ответ: ________________.

Задание 3.2.8.

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12 & 6 = 1100₂ & 0110₂ = 0100₂ = 4.

а) Для какого наименьшего неотрицательного целого числа А формула тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной х)?

Ответ: ________________.

B) Для какого наименьшего неотрицательного целого числа А формула тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

Ответ: ________________.

c) Для какого наименьшего неотрицательного целого числа А формула тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

Ответ: ________________.

d) Для какого наибольшего неотрицательного целого числа А формула тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

Ответ: ________________.