Алгебра 7 класс - Технологические карты уроков по учебнику А. Г. Мордковича - 2016
Урок 18. ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК - ЛИНЕЙНАЯ ФУНКЦИЯ
|
Тип урока: изучение нового материала |
|||||||
|
Задачи: создать условия для развития умений приводить примеры линейных уравнений с двумя переменными, определять, является ли пара чисел решением данного линейного уравнения с двумя переменными, строить график линейного уравнения с двумя переменными |
|||||||
|
Планируемые результаты |
|||||||
|
Предметные: познакомятся с понятиями линейного уравнения с двумя переменными и его графиком; научатся строить график линейного уравнения с двумя переменными |
Метапредметные: познавательные - проводить сравнение, сериацию и классификацию по заданным критериям; регулятивные - вносить необходимые коррективы в действие после его завершения на основе его и учета характера сделанных ошибок; коммуникативные - учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве |
Личностные: формировать интерес к изучению темы и желание применять приобретенные знания |
|||||
|
Образовательные ресурсы: 1) Презентации по математике. URL: http://ppt4web.ru/matematika 2) Видеоуроки. URL: http://intemeturok.ru/ |
|||||||
|
Организационная структура урока |
|||||||
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности |
||||
|
1. Организационный этап |
|||||||
|
2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся |
|||||||
|
3. Изучение нового материала |
Теоретический материал темы “Линейное уравнение с двумя переменными и его график” (учебник, с. 39-42) |
Ведение конспекта: составление учащимися алгоритма построения графика линейного уравнения с двумя переменным РМ. Устно: № 7.1-7.6 |
Воспроизводить теорию, прослушанную с заданной степенью свернутости; участвовать в диалоге, подбирать аргументы для объяснения ошибки |
||||
|
4. Первичное закрепление нового материала |
Организует индивидуальную работу для учащихся, которые освоили тему. Предлагает учащимся, работающим у доски, ответить на дополнительные вопросы РМ |
У доски (а, б) |
№ 7.10-7.14 |
||||
|
Индивидуально (в, г) |
|||||||
|
5. Повторение |
Задачник: № 7.30 |
||||||
|
6. Итоги урока |
Предлагает учащимся ответить на вопрос: - Какие этапы урока вы считаете наиболее удачными и почему? |
Отвечают по желанию |
|||||
|
7. Домашнее задание |
Учебник: прочитать § 7, с. 39-42; задачник: № 7.15, 7.10, 7.25, 7.26 |
Задание с параметром РМ |
|||||
Ресурсный материал к уроку 18
1. Алгоритм построения графика линейного уравнения с двумя переменным:
1. Начертить координатные оси, подписать их и отметить единичный масштаб.
2. В линейном уравнении рассмотреть х = 0 и решить полученное уравнение относительно у. Отметить полученную точку на графике.
3. В линейном уравнении рассмотреть у = 0 и решить полученное уравнение относительно х. Отметить полученную точку на графике.
4. При необходимости взять дополнительное произвольное значение х и решить полученное уравнение относительно у. Отметить полученную точку на графике.
5. Соединить полученные точки, продолжить график за них. Подписать получившуюся прямую.
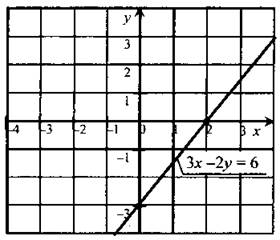
Пример: Построить график уравнения 3х - 2у = 6.
Положим, х = 0, тогда -2у = 6 ⇒ у = -3. Положим, у = 0, тогда 3х = 6 ⇒ х = 2.
Отмечаем полученные точки на графике, проводим через них прямую и подписываем её.
Посмотрите на рисунок, график должен получиться именно таким.
2. Дополнительные вопросы к теоретическому материалу:
1) Дать определение понятию линейного уравнения с двумя переменными.
2) Дать определение понятию корня линейного уравнения.
3) Дать определение понятию графика линейного уравнения.
4) Определить из данных уравнений линейные уравнения с двумя переменными:
![]()
5) Для уравнения вида 2х - 5у + 3 = 0 определить корни из данных пар чисел: (2; 1), (1; 1), (6; -3), (6; 3), (-2; 1).
6) Для данного уравнения 2х - 5у + 3 = 0 предложить пару чисел, которая является его решением, и предложить пару чисел, не являющуюся решением для данного уравнения.
4) Найти для каждого из уравнений значения, соответствующие заданному значению х = 0 и у = 0:
![]()
3. Задание с параметром.
1) При каких целых значениях а корень уравнения является целым числом, которое делится нацело на 2:
![]()
2) При каких значениях b корень уравнения будет меньше, чем b:
а) 3х = b; б) 3х = 2b?