Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
ПЕРПЕНДИКУЛЯР К ПРЯМОЙ. МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА - ТРЕУГОЛЬНИКИ
|
Цель деятельности учителя |
Создать условия для введения понятий перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника, доказательства теоремы о перпендикуляре, обучения построению медианы, биссектрисы и высоты треугольника |
||
|
Термины и понятия |
Треугольник, медиана, биссектриса, высота, перпендикуляр |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира; приобретают навыки геометрических построений |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Задания для фронтальной работы |
||
|
I этап. Актуализация знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить правильность выполнения домашнего задания |
(Ф/И) 1. Проверить правильность выполнения домашнего задания. Для этого к доске вызываются двое учеников, которые демонстрируют выполнение заданий. Остальные учащиеся задают вопросы. 2. Проанализировать ошибки, допущенные в самостоятельной работе |
||
|
II этап. Учебно-исследовательская деятельность |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Ввести понятия медианы, биссектрисы и высоты треугольника в ходе практической деятельности |
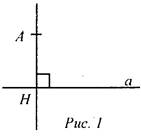
(Ф/И) 1. Выполнение практического задания (учитель это же задание выполняет на доске). - Начертите прямую а и отметьте точку А, не лежащую на прямой (рис. 1).
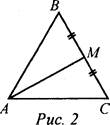
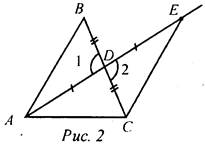
- Через точку А проведите прямую, перпендикулярную прямой а. Точку пересечения прямых обозначьте Н. -Запишите в тетрадях: “Отрезок АН - перпендикуляр, проведенный из точки А к прямой а, если: 1) АН ⊥ а; 2) А ∉ а, Н ∈ а”. Теорема о перпендикуляре: Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и при том только один. Дано: а - прямая, точка А ∉ а. Доказать: 1) из точки А к прямой а можно провести перпендикуляр; 2) из точки А к прямой а можно провести единственный перпендикуляр. Доказательство: см. п. 16 учебника. 2. Определение: Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника. На доске и в тетрадях рисунок (рис. 2) и запись: AM - медиана ΔАВС, если М ∈ ВС, ВМ = МС.
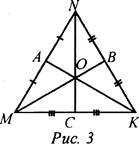
- Начертите ΔMNK, постройте его медианы. (На доске это же задание выполняет один из учащихся по указанию учителя.) На доске и в тетрадях рисунок (рис. 3) и запись: MB, КА, NC - медианы AMNK. MB ∩ КА ∩ NC = О.
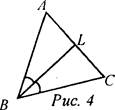
3. Определение: Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. На доске и в тетрадях рисунок (рис. 4) и запись: BL - биссектриса ΔАВС, если L ∈ АС, ∠ABL = ∠CBL.
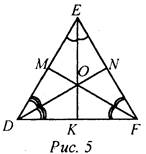
- Начертите ADEF, постройте его биссектрисы. (На доске это же задание выполняет один из учащихся по указанию учителя.) На доске и в тетрадях рисунок (рис. 5) и запись: DN, ЕК, FM - биссектрисы ΔDEF. DN ∩ EK ∩ ЕМ = О.
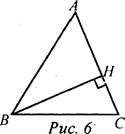
4. Определение: Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника. На доске и в тетрадях рисунок (рис. 6) и запись: ВН - высота ΔАВС, если ВН ⊥ АС, Н ∈ АС.
- Начертите остроугольный, прямоугольный и тупоугольный треугольники и постройте их высоты.
(К доске вызвать трех учеников, первый из них строит высоты для остроугольного треугольника, второй — для прямоугольного, третий — для тупоугольного.) |
||
|
III этап. Решение задач на закрепление изученного материала |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать навыки построения медиан, биссектрис и высот |
(П) Выполнить в парах № 101, 102, 103. (Ф/И) Выполнить на доске и в тетрадях № 105 и 106 |
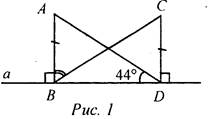
№ 105. Дано: А, С по одну сторону от а, АВ ⊥ a, CD ⊥ а, АВ = CD, ∠ADB = 44°. Доказать: ∠ABD = ∠CDB. Найти: ∠ABC.
Доказательство: 1) В ΔABD и ΔCDB BD - общая, АВ = CD (по усл.). ∠B = ∠D = 90° (так как АВ ⊥ a, CD ⊥ а). Таким образом, ΔABD = ΔCDB (по двум сторонам и углу между ними). 2) Из п. 1 следует, что ∠CBD = ∠ADB = 44°, тогда ∠ABC = ∠ABD - ∠CBD, ∠ABC = 90° - 44° = 46°. № 106. Дано: ΔАВС, AD - медиана, AD = DE, ∠ACD = 56°, ∠ABD = 40°. Доказать: ΔABD = ΔECD. Найти: ∠ACE.
Доказательство: 1) Рассмотрим ΔABD и ΔECD. BD = DC (по усл.), AD = DE (по усл.), ∠1 = ∠2 - вертикальные, ΔABD = ΔECD (по двум сторонам и углу между ними), тогда ∠ABD = ∠ECD (по определению равных треугольников), ∠ECD = 40°. 2) ∠АСЕ = ∠ACD + ∠ECD = 56° + 40° = 96° |
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Какими свойствами обладают медианы, биссектрисы и высоты треугольника? - Составьте синквейн к уроку |
(И) Домашнее задание: изучить пункты 16 и 17; ответить на вопросы 5-9 на с. 50; решить № 100 |
||