Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ - ТРЕУГОЛЬНИКИ
|
Цель деятельности учителя |
Создать условия для повторения и закрепления изученного ранее материала, изучения второго признака равенства треугольников и выработки навыков использования первого и второго признаков равенства треугольников при решении задач; способствовать развитию логического мышления учащихся |
||
|
Термины и понятия |
Треугольник, прилежащие углы |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию) |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Чертежи к задачам. • Задания для фронтальной и индивидуальной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать навык решения задач по готовым чертежам с целью повторения первого признака равенства треугольников |
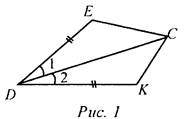
(Ф/И) 1. Проверка домашнего задания. 2. Решение задач (устно). 1) На рис. 1 DE = DK, ∠1 = ∠2. Найдите ЕС, ∠DCK и ∠DKC, если КС = 1,8 дм; ∠DCE = 45°, ∠DEC = 115°.
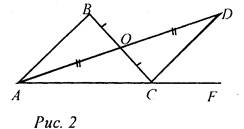
2) ОВ = ОС, АО = DO; ∠ACВ = 42°, ∠DCF = 68°. Найдите ∠ABC.
|
||
|
II этап. Изучение нового материала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Организовать выполнение практической работы с целью подготовки к восприятию новой темы |
(Ф/И) Практическая работа. Начертите ΔMNK - такой, что ΔMNK = ΔАВС, если известно, что АВ = 4 см, ∠A = 54°, ∠B = 46°. Построение: 1) отложить отрезок MN = 4 см, так как ΔMNK = ΔАВС, а значит, MN = АВ; 2) построить ∠NMP = 54°; 3) построить ∠MNE = 46° по ту же сторону от прямой MN, что и ∠NMP; 4) МР ∩ NE = К, ΔMNK - искомый. (Идет обсуждение практического задания. Учитель задает вопросы, учащиеся отвечают на них.) - Будут ли равны ΔАВС и ΔMNK, если АВ = MN, ∠A = ∠M, ∠B = ∠N? (Да, ΔАВС = ΔMNK.) - Докажите равенство треугольников АВС и MNK. Дано: ΔABC, ΔMNK, АВ = MN, ∠A = ∠M, ∠B = ∠N. Доказать: ΔАВС = ΔMNK. Доказательство: Наложим ΔАВС на ΔMNK так, чтобы АВ совместилось с MN, а вершины С и К лежали по одну сторону от MN. Так как по условию задачи АВ = MN, то вершина Aсовместится с вершиной М, а вершина В - с вершиной N. Луч АС совместится с лучом МК, так как ∠A = ∠M, а луч ВС совместится с лучом NK, так как ∠B = ∠N. Точка пересечения лучей АС и ВС совместится с точкой пересечения лучей МК и NK, то есть точка С совместится с точкой К. Получили, что треугольники АВС и MNK полностью совместились, а это значит, что ΔАВС = ΔMNK. - Итак, мы только что доказали второй признак равенства треугольников. Сформулируйте его и дайте ему название. Определение: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. - Второй признак равенства треугольников можно назвать признаком равенства треугольников по стороне и прилежащим к ней углам |
||
|
III этап. Решение задач на закрепление изученного материала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать навыки решения задач по изученной теме |
(Ф/И) 1. Решить задачи по готовым чертежам (устно).
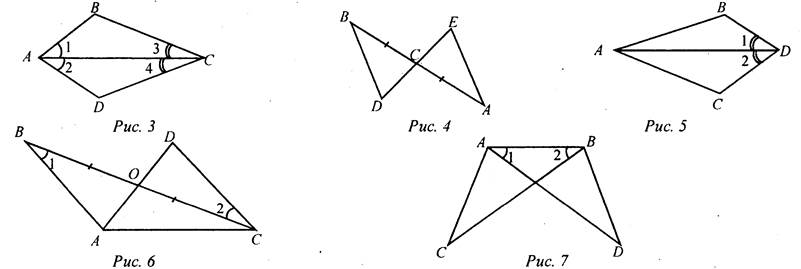
1) На рис. 3 ∠1 = ∠2 и ∠3 = ∠4. Докажите, что ΔАВС = ΔADC. 2) На рис. 4 АС = СВ, ∠A = ∠B. Докажите, что ΔBCD = ΔАСЕ. 3) На рис. 5 AD - биссектриса угла ВАС, ∠1 = ∠2. Докажите, что ΔABD = ΔACD. 4) На рис. 6 ВО = ОС, ∠1 = ∠2. Укажите равные треугольники на этом рисунке. 5) На рис. 7 ∠1 = ∠2, ∠CAB = ∠DBA. Укажите равные треугольники на этом рисунке. 2. Решить задачу № 121 (самостоятельно). 3. Решить задачу № 126 (по рис. 74 учебника на с. 40). 4. Решить задачу № 127 (записать решение этой более сложной задачи на доске и в тетрадях). № 127.
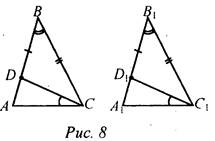
Дано: ΔАВС, ΔА1В1С1, АВ = А1В1, ВС = В1С1, ∠B = ∠B1; D ∈ АВ, D1 ∈ А1В1, ∠ACD = ∠A1C1D1. Доказать: ΔBCD = ΔB1C1D1. Доказательство: 1) Рассмотрим ΔАВС и ΔА1В1С1: АВ = A1B1 (по усл.), ВС = В1С1 (по усл.), ∠B = ∠B1 (по усл.), ΔАВС = ΔА1В1С1 (по двум сторонам и углу между ними), тогда АС = А1С1, ∠A = ∠A1, ∠C = ∠C1 (по определению равных треугольников). 2) Рассмотрим ΔBCD и ΔB1C1D1, ВС = В1С1, ∠BCD = ∠B1C1D1 (так как ∠BCD = ∠C - ∠ACD, ∠B1C1D1 = ∠C1 - ∠A1C1D1). ∠B = ∠B1 (по усл.). ΔBCD = ΔB1C1D1 (по стороне и двум прилежащим углам), что и требовалось доказать |
||
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Что нового узнали на уроке? - Кто может повторить второй признак равенства треугольников? - Составьте синквейн по теме урока |
(И) Домашнее задание: выучить доказательство теоремы из п. 19; решить задачи № 124, 125, 128 |
||