Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ - ТРЕУГОЛЬНИКИ
|
Цель деятельности учителя |
Создать условия для изучения третьего признака равенства треугольников и его закрепления в ходе решения задач, отработки у учащихся умения применять Изученные теоремы при решении задач |
||
|
Термины и понятия |
Треугольник, углы, стороны |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию) |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Задания для фронтальной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить уровень сформированности теоретических знаний |
(Ф/И) 1. Проверить домашнее задание. Для этого можно к доске вызвать троих учащихся. 2. У доски доказать второй признак равенства треугольников |
||
|
II этап. Изучение новой темы |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Доказать третий признак равенства треугольников |
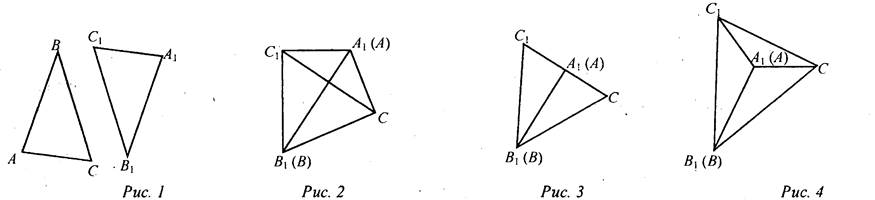
(Ф) Учитель сам читает формулировку третьего признака равенства треугольников и доказывает его до рассмотрения первого случая. Доказательство первого случая можно провести в виде беседы сучащимися. Третий признак равенства треугольников: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Дано: ΔАВС, ΔА1В1С1, АВ = А1В1, ВС = В1С1, АС = А1С1. Доказать: ΔАВС = ΔА1В1С1.
Доказательство: Приложим ΔАВС к ΔА1В1С1 (см. рис. 1), так чтобы сторона АВ совместилась со стороной А1В1 (они совместятся, так как по условию теоремы АВ = А1В1), а вершины С и С1, находились по разные стороны от прямой А1В1. Возможны три случая 1) луч СС1 проходит внутри угла (рис. 2); 2) луч СС1 совпадает с одной из сторон угла В1С1А1 (рис. 3) 3) луч СС1 проходит вне угла В1С1А1 (рис. 4). Докажем первый случай. - Что вы можете сказать о треугольниках С1А1С и С1В1С1 (Они равнобедренные.) - Равны ли углы А1С1В1 и АСВ? Почему? (∠A1C1B1 = ∠ACB, так как ∠A1C1B1 = ∠A1C1C + ∠B1C1C, ∠ACB = ∠ACC1 + ∠BCC1, a ∠A1C1C = ∠ACC1, ∠B1C1C = ∠BCC1, как углы при основании равнобедренных треугольников.) - Равны ли ΔАВС и ΔА1В1С1 (ΔАВС = ΔА1В1С1 по двум сторонам и углу между ними, так как АС = А1С1, СВ = С1В1, ∠ACB = ∠A1C1B1 по доказанному.) - Итак, ΔАВС = ΔА1В1С1. Далее можно предложить учащимся доказать равенство треугольников АВС и А1В1С1 во втором или третьем случае, а оставшийся случай рассмотреть дома. Доказательство второго случая. АВ1С1С — равнобедренный с основанием СС1, так как В1С1 = ВС = В1С по условию теоремы. В1А1 - медиана ΔВ1С1С, так как С1А1 = АС по условию теоремы, а АС = А1С. Медиана, проведенная к основанию равнобедренного треугольника, является его биссектрисой, то есть ∠C1B1A1 = ∠CBA. ΔАВС = ΔА1В1С1 по двум сторонам и углу между ними (АВ = А1В1, ВС = В1С1 по условию теоремы, ∠CAB = ∠C1B1A1 по доказанному). Доказательство третьего случая. ΔВ1С1С - равнобедренный с основанием СС1, так как В1С1 = ВС по условию теоремы. ∠B1C1C = ∠BCC1, как углы при основании равнобедренного треугольника. ΔА1С1С- равнобедренный с основанием СС1, так как А1С = АС по условию теоремы. ∠A1C1C = ∠ACC1, как углы при основании равнобедренного треугольника. ∠B1C1A1 = ∠BCA, так как ∠B1C1A1 = ∠B1C1C - ∠A1C1C, ∠BCA = ∠BCC1 - ∠ACC1, a∠B1C1C = ∠BCC1 и ∠A1C1C = ∠ACC1 по доказанному. ΔАВС = ΔA1B1C1 no двум сторонам и углу между ними (ВС = В1С1, АС = А1С и ∠BCA = ∠B1C1A1). Далее можно ввести понятие жесткой фигуры или предложить учащимся самостоятельно прочитать с. 40 учебника - на уроке или дома |
||
|
III этап. Решение задач на закрепление изученной темы |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
На простых задачах отработать применение третьего признака равенства треугольников |
(Ф/И) 1. Найдите пары равных треугольников и докажите их равенство.
2. Решить № 135 (устно). 3. Решить № 138 на доске и в тетрадях |
||
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - С чем познакомились на уроке? - Задайте три вопроса по теме урока |
(И) Домашнее задание: повторить п. 15—19, изучить п. 20; решить № 134, 136, 137 |
||