РЕШЕНИЕ ЗАДАЧ - Урок 3 - ТРЕУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для закрепления навыков решения задач на применение признаков равенства треугольников, на построение с помощью циркуля и линейки

Термины и понятия

Треугольники, окружность, дуга окружности

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют применять изученные понятия, методы для решения задач практического характера

Познавательные: умеют выбирать и создавать алгоритмы для решения учебных математических проблем.

Регулятивные: умеют самостоятельно ставить цели, понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные ресурсы

• Задания для письменной работы.

• Чертежи к задачам

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Проверить выполнение домашнего задания

(Ф/И)

1. Проверка домашнего задания.

2. Понятие трисекции угла.

- Трисекция угла — задача о делении заданного угла на три равные части построением с помощью циркуля и линейки. Иначе говоря, необходимо построить трисектрисы угла - лучи, делящие угол на три равные части. Наряду с задачами о квадратуре круга и удвоении куба трисекция угла является одной из классических неразрешимых задач на построение, известных со времен Древней Греции.

3. Письменная работа на проверку навыков решения задач на построение с помощью циркуля и линейки.

Вариант I

1) Отложить от данного луча угол, равный данному.

2) Построить середину данного отрезка.

Вариант II

1) Построить биссектрису данного неразвернутого угла.

2) Построить прямую, проходящую через данную точку й перпендикулярную к прямой, на которой лежит данная точка

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

(Ф/И) Организует деятельность учащихся.

1. Решение задач по готовым чертежам.

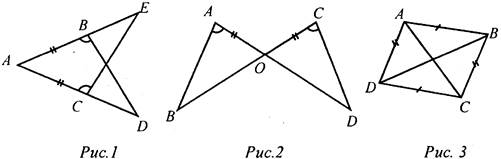
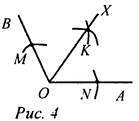
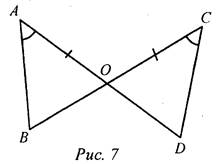
1) Рис. 1.

а) Дано: АВ = АС, ∠ACE = ∠ABD.

Доказать: ΔАСЕ = ΔABD.

б) Дано: АЕ = 15 см, ЕС = 10 см, АС = 1 см.

Найти: стороны ΔABD.

2) Рис. 2.

Дано: АО = ОС, ∠BAO = ∠DCO.

Доказать: АВ = CD.

3) Рис. 3.

Дано: АВ = DC, AD = ВС, Р_АВС = 15 см, Р_ABCD = 20 см.

Найти: АС.

2. Решение задач № 152 и 165 на доске и в тетрадях

№ 152.

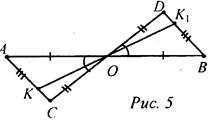
Построение:

1) Построим окружность с центром О и произвольным радиусом. Окружность пересечет стороны угла в точках М и N.

2) Построим 2 окружности с одинаковым радиусом больше половины длины отрезка MN. Одна окружность с центром М, а другая с центром N. Эти окружности пересекутся в точке К.

3) Соединим лучом О и К - это и есть искомый луч, который разделил ∠AOB на ∠AOX и ∠BOX.

№ 165.

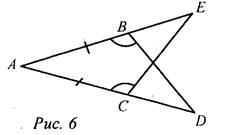
Дано: АВ ∩ CD = О, АО = ОВ, СО = OD, К ∈ АС, К₁ ∈ BD, АК = ВК₁.

Доказать: а) ОК = ОК₁; б) О ∈ КК₁.

Доказательство:

1) Рассмотрим ΔАОС и ΔBOD. АО = ОВ (по усл.), СО = OD (по усл.), ∠AOC = ∠BOD (вертикальные), ΔАОС = ΔBOD (по двум сторонам и углу между ними), тогда ∠A = ∠B (по определению равных треугольников).

2) Рассмотрим ΔАКО и ΔВК₁О. АК = BK₁ (по усл.), ∠A = ∠B (из п. 1), ΔАКО и ВК₁О (по двум сторонам и углу между ними), тогда ∠AOK= ∠BOK\, КО = OK (по определению равных треугольников).

3) АВ - отрезок по условию. ∠AOK = ∠BOK₁ (из п. 2), тогда ∠AOK и ∠BOK₁ - вертикальные, значит О, К, К₁ лежат на одной прямой

III этап. Самостоятельная работа

Цель деятельности

Задания для самостоятельной работы

Проверить уровень сформированности теоретических знаний

(И) Работа выполняется на листках и сдается на проверку учителю.

Вариант I

1. На рисунке АВ = АС и ∠ACE = ∠ABD.

1) Докажите, что ΔАСЕ = ΔABD.

2) Найдите стороны треугольника ABD, если АЕ = 15 см, ЕС = 10 см, АС = 7см.

2. Известно, что в треугольниках АВС и А₁В₁С₁ ∠А = ∠А₁, АВ = А₁В₁, АС = А₁С₁.

На сторонах ВС и В₁С₁ отмечены точки К и К₁, такие, что СК = С₁К₁.

Докажите, что ΔАВК = ΔА₁B₁K₁.

Вариант II

1. На рисунке АО = СО и ∠BAО = ∠DCO.

1) Докажите, что ΔАОВ = ΔDCO.

2) Найдите углы ΔАОВ, если ∠OCD = 37°, ∠ODC = 63°, ∠COD = 80°.

2. Известно, что в треугольниках АВС и А₁В₁С₁ ∠B = ∠B₁, AB = А₁В₁ и ВС = В₁С₁.

На сторонах АС и А₁С₁ отмечены точки D и D₁, так что AD = A₁D₁.

Докажите, что ΔBDC = ΔB₁D₁C₁

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что повторили на уроке?

- Оцените свою работу на уроке

(И) Домашнее задание: повторить материал п. 15-20; решить № 158, 166