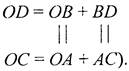Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
РЕШЕНИЕ ЗАДАЧ - Урок 4 - ТРЕУГОЛЬНИКИ
|
Цели деятельности учителя |
Создать условия для закрепления навыков решения задач на применение признаков равенства треугольников, проверки знаний учащихся, подготовки учащихся к предстоящей контрольной работе |
|||
|
Термины и понятия |
Треугольники, окружность |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют применять изученные понятия, результаты, методы для решения задач практического характера |
Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
|||
|
Образовательные ресурсы |
• Карточки для устного опроса. • Задачи для фронтальной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить уровень сформированности теоретических знаний |
(И) 1. Анализ и сообщение результатов самостоятельной работы. 2. Устный опрос учащихся у доски по карточкам (см. Ресурсный материал) |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать навыки решения задач |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу. В равнобедренном треугольнике MDK длина основания МК относится к длине боковой стороны MD как 3:4. Найдите стороны этого треугольника, если периметр его равен 33 см. 2. Решить задачу самостоятельно. В равнобедренном треугольнике длина боковой стороны относится к длине основания как 2:3. Найдите стороны треугольника, если периметр его равен 28 см. (Г) 3. Решить № 175 с вынесением решения на доску и обсуждением. Описание способа построения биссектрисы угла с опорой на данную задачу. 1) Построить окружность с центром в вершине угла произвольного радиуса. Окружность пересечет стороны угла в точках А и В. 2) Построить окружности с центрами в точках А и В также произвольного радиуса. Окружность с центром А и радиусом Rпересечет сторону угла в точке С, аналогично, окружность с центром В и радиусом R пересечет сторону угла в точке D. 3) Построим отрезки AD = ВС. 4) Отрезки пересекутся в точке Е. 5) Соединим лучом вершину угла с точкой Е. Получим луч ОЕ - искомая биссектриса |
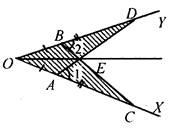
1. Решение: Пусть на одну часть приходится х см, тогда МК = 3х cm, MD = DK = 4х см. По условию Р = 33 см, значит, 3х + 4х + 4х = 33; 11х = 33; х = 3. МК = 9 см, MD = DK = 12 см. Ответ: 9 см; 12 см; 12 см. № 175. Дано: ОА = OB, АС = BD. Доказать: ОЕ - биссектриса.
Доказательство: 1) Рассмотрим ΔAOD и ΔBCО. ∠O - общий, ОА = ОВ (по усл.), OD = ОС (так как
ΔADO = ΔВСО (по двум сторонам и углу между ними), тогда ∠D = ∠C, ∠OAD = ∠OBC (по определению равных треугольников). 2) ∠OAD и ∠1 - смежные, значит, ∠1 = 180° - ∠OAD. ∠OBC и ∠2 - смежные, значит, ∠2 = 180° - ∠OBC, тогда ∠1 = ∠2. 3) Рассмотрим ΔBED и ΔАЕС. ∠1 = ∠2 (из п. 2), ∠D = ∠C (из п. 1), BD = AC (по усл.), ΔBED = ΔАЕС (по стороне и двум прилежащим углам), тогда DE = ЕС (по определению равных треугольников). 4) Рассмотрим ΔOED и ΔОСЕ. ОЕ - общая, OD = ОС (из п. 1), DE = ЕС (из п. 3), значит, ΔOED= ΔОЕС (по трем сторонам), тогда ∠DOE = ∠COE (по определению равных треугольников), значит, ОЕ - биссектриса, что требовалось доказать |
||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - Оцените свою работу на уроке. - Оцените свою работу в группе |
(И) Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 15-23; решить задачи № 170, 171 |
|||
Ресурсный материал
Карточки для устного опроса
Вариант I
1. Сформулируйте первый признак равенства треугольников.
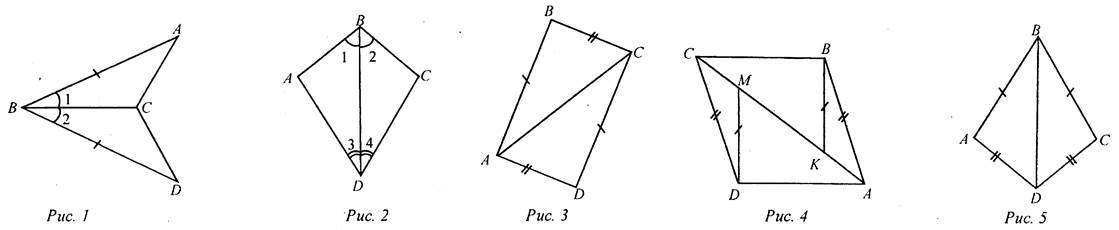
2. На рисунке 1 АВ = DB, ∠1 = ∠2. Докажите, что ΔАВС = ΔDBC.
3. В треугольниках АВС и А1В1С1 АВ = А1В1 АС = А1С1, ∠A = ∠A1. На сторонах АС и А1С1 отмечены точки D и D1 так, что CD = C1D1. Докажите, что ΔABD = ΔA1B1D1.
Вариант II
1. Сформулируйте второй признак равенства треугольников.
2. На рисунке 2 ∠1 = ∠2, ∠3 = ∠4. Докажите, что AABD = ACBD.
3. В треугольниках АВС и А1В1С1 проведены биссектрисы AD и A1D1. Докажите, что ΔАВС = ΔА1В1С1, если DC = D1C1, ∠C = ∠C1, ∠ADC = ∠A1D1C1.
Вариант III
1. Сформулируйте третий признак равенства треугольников.
2. На рисунке 3 АВ = DC, ВС = AD. Докажите, что ΔАВС = ΔCDA.
3. На рисунке 4 АВ = DC, ВК = DM, AM = СК. Докажите, что ΔADM = ΔСВК.
Вариант IV
1. Сформулируйте свойство углов равнобедренного треугольника.
2. На рисунке 5 АВ = ВС, AD = DC. Докажите, что ΔBAD = ΔBCD.
3. В равнобедренном треугольнике АВС на основании АС взяты точки D и Е так, что AD = СЕ. Докажите, что треугольник DBE равнобедренный.
Вариант V
1. Сформулируйте свойство биссектрисы, проведенной к основанию равнобедренного треугольника.
2. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса BD, ∠ABD = 37°, АС = 25 см. Найдите ∠B, ∠BDC и DC.
3. В равнобедренном треугольнике CDE с основанием DE проведена биссектриса CF. Найдите CF, если периметр треугольника CDE равен 84 см, а периметр треугольника CFE равен 56 см.