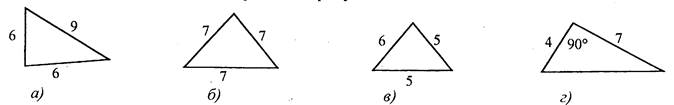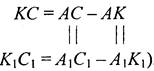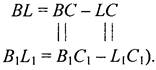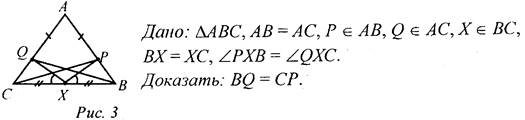Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
РЕШЕНИЕ ЗАДАЧ. ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ - ТРЕУГОЛЬНИКИ
|
Цель деятельности учителя |
Создать условия для закрепления навыков решения задач на применение признаков равенства треугольников, для проверки знаний учащихся, подготовки к предстоящей контрольной работе |
||
|
Термины и понятия |
Треугольники, окружность |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют применять изученные понятия, методы для решения задач практического характера |
Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Чертежи к заданиям |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Повторить признаки равенства треугольников |
(Ф/И) 1. Обсудить вопросы учащихся по домашнему заданию. 2. Выполнить задание. Равносторонний треугольник изображен на рисунке...
3. Выполнить задание. Треугольники, изображенные на рисунке... а) равны по двум сторонам и углу между ними; б) равны по стороне и двум прилежащим к ней углам; в) равны по трем сторонам; г) не равны
|
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать навыки решения задач |
(Ф/И) Организует деятельность учащихся: решение задач 177, 178, 179 на доске и в тетрадях |
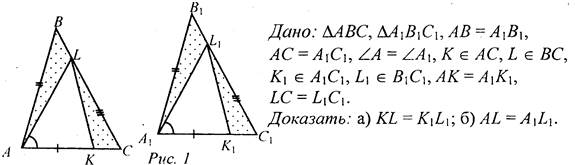
№ 177.
Доказательство: 1) Рассмотрим ΔАВС и ΔА1В1С1. АВ = А1В1 (по усл.), АС = А1С1 (по усл.), АА = АА1 (по усл.), ΔАВС = ΔА1В1С1(по двум сторонам и углу между ними), тогда АВ = АВ1, АС = АС1, ВС = В1С1 (по определению равных треугольников). 2) Рассмотрим ΔLCK и ΔL1C1K1, LC = L1C1 (по усл.), ∠С = ∠C1 (из п. 1), КС = С1К1 (так как
ΔLCK = ΔL1C1K1 (по двум сторонам и углу между ними), тогда LK = L1K1 (по определению равных треугольников). 3) Рассмотрим ΔABL и ΔA1B1L1, АВ = А1В1 (по усл.), АВ = АВ1 (из п. 1), BL = B1L1 (так как
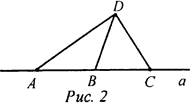
ΔABL = ΔА1В1L1 (по двум сторонам и углу между ними), тогда AL = A1L1 (по определению равных треугольников), что и требовалось доказать. № 178. Дано: А, В, С ∈ a, D ∉ а. Доказать: по крайней мере, два из трех отрезков AD, BD и CD не равны друг другу.
Доказательство: 1) Предположим, что AD = BD = CD. 2) Следовательно, ΔABD, ΔBDC и ΔADC - равнобедренные, значит, ∠1 = ∠2, ∠3 = ∠4, ∠1 = ∠4. Из всех трех равенств следует, что ∠2 = ∠3, а так как ∠2, ∠3 - смежные, то ∠2 = ∠3 = 90°, следовательно, получим в ΔABD: ∠А = ∠В = 90°, в A BCD: ∠В = ∠С = 90°, в ΔADC: ∠А = ∠С = 90°. 3) Это противоречит теореме о том, что через точку, не лежащую на прямой, можно провести единственный перпендикуляр к данной прямой, а у нас получилось 3. 4) Вывод: наше предположение неверно, следовательно, по крайней мере, два из трех отрезков AD, BD и CD не равны друг другу, что и требовалось доказать. № 179.
Доказательство: 1) Так как ΔАВС - равнобедренный, ∠В = ∠С. 2) Рассмотрим ΔCQX и ΔВРХ. СХ = ВХ (по усл.), ∠QХC = ∠РХВ (по усл.), ∠C = ∠B (из п. 1). ΔCQX = ΔВРХ (по стороне и двум прилежащим углам), тогда CQ = РВ, QX = ХР (по определению равных треугольников). 3) Рассмотрим ΔCQB и ΔВРС. CQ = РВ (из п. 2), СВ - общая, ∠C = ∠В (из п. 1), ΔСОВ = ΔВРС (по двум сторонам и углу между ними), тогда QB = СР, что и требовалось доказать |
|
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Какие трудности у вас возникали в процессе решения задач? - Составьте синквейн к уроку |
(И) Домашнее задание: решить № 180, 182, 184 |
||