Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год

КОНТРОЛЬНАЯ РАБОТА № 2 - ТРЕУГОЛЬНИКИ

Цель деятельности учителя	Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала
Термины и понятия	Признаки равенства треугольников, равнобедренный треугольник, равносторонний треугольник, медианы, биссектрисы, высоты треугольника
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности		Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для контрольной работы
I этап. Выполнение контрольной работы
Цель деятельности	Задания для контрольной работы
Проверить уровень знаний, умений и навыков по изученному материалу	(И) Учащиеся выполняют задания контрольной работы (см. Ресурсный материал)
II этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) - Что выполняли на уроке? - Какие задания вызвали затруднения? Почему? - Как оцениваете свою работу на уроке?		(И) Домашнее задание: повторить материал пунктов 2-21

Ресурсный материал

Контрольная работа

Вариант I

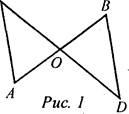
1. Дано: АО = ВО, СО = DO, СО = 5 см, ВО = 3 см, BD = 4 см (рис. 1).

Найти: периметр ΔСАО.

2. В равнобедренном треугольнике АВС точки К и М являются серединами боковых сторон АВ и BС соответственно. BD - медиана треугольника. Докажите, что ΔBKD = ΔBMD.

3. Даны неразвернутый угол и отрезок. На сторонах данного угла постройте точки, удаленные от вершины угла на расстояние, равное половине данного отрезка.

4*. Прямая МК разбивает плоскость на две полуплоскости. Из точек М и К в разные полуплоскости проведены равные отрезки МА и КВ, причем ∠AMK = ∠BKM. Какие из высказываний верные?

а) ΔАМВ = ΔАКВ;

б) ∠AKM = ∠BMK;

в) ΔMКА = ΔКМВ;

г) ∠AMB = ∠KMB.

Вариант II

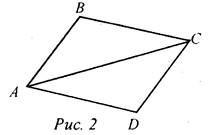
1. Дано: АВ = CD, ВС = AD, АС = 1 см, AD = 6 см, АВ = 4 см (рис. 2).

Найти: периметр ΔADC.

2. В равнобедренном АВС точки К и М являются серединами боковых сторон АВ и ВС соответственно. BD - медиана треугольника. Докажите, что ΔAKD = ΔCMD.

3. Даны неразвернутый угол и отрезок. На биссектрисе данного угла постройте точку, удаленную от вершины угла на расстояние, равное данному отрезку.

4*. Прямая АВ разбивает плоскость на две полуплоскости. Из точек А и В в разные полуплоскости проведены равные отрезки AD и ВС, причем ∠BAD = ∠ABC. Какие из высказываний верные?

a) ΔCAD = ΔBDA;

б) ∠DBA = ∠CAB;

в) ∠BAD = ∠BAC;

г) ∠ADB = ∠BCA.