Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
РАБОТА НАД ОШИБКАМИ - ТРЕУГОЛЬНИКИ
|
Цель деятельности учителя |
Создать условия для устранения пробелов в знаниях учащихся; совершенствовать навыки решения задач по теме “Треугольники” |
||
|
Термины и понятия |
Треугольники, окружность |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют применять изученные понятия, результаты, методы для решения задач практического характера |
Познавательные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, разрешать конфликты на основе согласования интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Задания для парной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проанализировать затруднения, возникшие при решении контрольной работы |
(Ф/И) 1. Сообщить учащимся результаты контрольной работы. 2. Решить задачи, вызвавшие наибольшее затруднение |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать навыки решения задач |
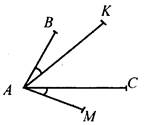
(П) Учащимся предлагается решить любые три задачи из представленных. Учитель выступает в роли консультанта. Задача 1. В равнобедренном треугольнике АВС с основанием АС проведены медианы АЕ и CD. Докажите, что: а) ΔАВЕ = ΔCBD; б) ΔDOE и ΔАОС - равнобедренные (О - точка пересечения АЕ и CD); в) ОВ - биссектриса ∠DOE. Задача 2. В равнобедренном ΔАВС с основанием АС на сторонах АВ и ВС отмечены соответственно точки М и N так, что ∠ACM = ∠CAN. Докажите, что: а) ΔMBN - равнобедренный; б) ВО ⊥ MN (О - точка пересечения AN и СМ). Задача 3. Треугольники АВС и DEF - равнобедренные и равные. Найти периметр ΔАВС, если DE = 4 см, EF = 5 см. Задача 4. Дано: АВ = AM, АС = АК, ∠BAK = ∠САМ.
Перечислите все пары равных треугольников с вершинами в точках А, В, К, С, М. Задача 5. На боковых сторонах равнобедренного треугольника во внешнюю сторону построены равносторонние треугольники. Докажите, что отрезки, соединяющие вершины равносторонних треугольников (отличные от вершин равнобедренного) с серединой основания равнобедренного треугольника, равны между собой |
||
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - В чем возникли затруднения? Почему? - Оцените свою работу и работу своего напарника |
(И) Домашнее задание: решить оставшиеся задачи |
||