РЕШЕНИЕ ЗАДАЧ - Урок 7 - ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

Цель деятельности учителя	Создать условия для приведения в систему знаний учащихся по изученной теме, для формирования у учащихся четкого понимания того, когда в задаче нужно применить признак параллельности двух прямых, а когда - свойство параллельных прямых; для подготовки к контрольной работе
Термины и понятия	Параллельные прямые, аксиома, свойства параллельных прямых
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию		Познавательные: владеют логическими действиями. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки, осуществляют контроль по результату и способу действия на уровне произвольного внимания и вносят необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Тест. • Задания для домашней работы
I этап. Активизация опорных знаний учащихся
Цель деятельности	Совместная деятельность
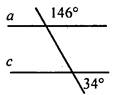
Систематизировать теоретические знания по теме	(Ф/И) 1. Ответить на вопросы по домашнему заданию. 2. Решить тест (каждое из заданий № 1, 2 оценивается в 4 балла). 1) Выберите верные утверждения. а) Параллельные лучи лежат на параллельных прямых. б) Если накрест лежащие углы равны, то прямые параллельны. в) Если при пересечении двух прямых секущей соответственные углы равны 122°, то прямые параллельны. г) Если прямая а перпендикулярна прямой с, а прямая с перпендикулярна прямой b, то прямые а и b пересекаются. 2. По данным рисунка докажите, что прямые с и а параллельны. Ответ: 1) а, б, в
II этап. Решение задач
Цель деятельности	Тестовые задания
Совершенствовать навыки решения задач	(Ф/И) Решить тест с самопроверкой (см. Ресурсный материал)
III этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
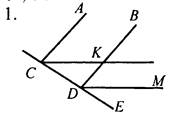
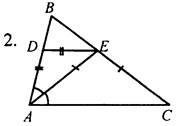
(Ф/И). - Оцените свою работу на уроке. - Составьте синквейн к уроку			(И) Домашнее задание: решить задачи (задачи даны на карточках). Дано: АС || BD, СК || DM, ∠ACК = 48°, ∠CDK в 3 раза больше ∠EDM. Найти: ZKDE. Дано: АЕ - биссектриса ΔABC, AD = DE, АЕ = ЕС, ∠ACB = 37°. Найти: ∠BDE.

Ресурсный материал

Тест

Часть 1

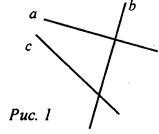
А1. На рисунке 1 секущей является прямая...

а) а;

б) с;

в) 6;

г) а или с.

А2. Для угла 4 накрест лежащим будет угол...

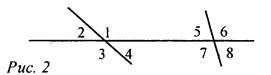
а) 2;

б) 5;

в) 6;

г) 7.

А3. На рисунке 3 углы 1 и 2 являются...

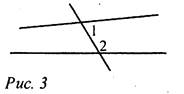
а) односторонними;

б) накрест лежащими;

в) соответственными;

г) смежными.

А4. Дан равносторонний треугольник BCD. Через вершину D провести прямых, параллельных прямой ВС.

а) можно две;

б) можно бесконечное множество;

в) нельзя ни одной;

г) можно одну.

А5. На рисунке 4 ∠1 = 54°. Прямые а и b будут параллельными, если ∠2 равен...

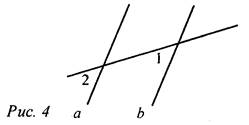
а) 54°;

б) 54° или 126°;

в) 126°;

г) 36°.

А6. Прямые будут параллельными на рисунке:

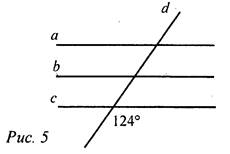
А7. На рисунке а, b, с пересечены секущей d. Параллельными прямыми будут прямые...

а) а и b;

б) b и с;

в) а и с;

г) а, b и с.

А8. Верным является высказывание:

а) Если две параллельные прямые пересечены третьей, то сумма накрест лежащих углов равна 180°.

б) Если при пересечении двух прямых секущей накрест лежащие углы в сумме составляют 180°, то прямые параллельны.

в) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

г) Если две прямые параллельны третьей прямой, то они перпендикулярны.

Часть 2

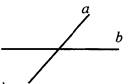
В1. Прямые а и b, изображенные на рисунке, являются ______________­_______________

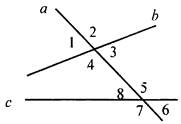
В2. Из всех углов, изображенных на рисунке, односторонними углами являются углы _______

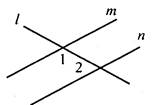
В3. На рисунке ∠1 = 135°, ∠2 = 45°. Тогда прямые m и n будут ____________________________

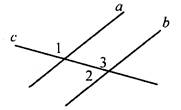
В4. На рисунке а || b, ∠3 = 108°. Тогда ∠1 = ________________

В5. На рисунке а || b, ∠1 на 50° меньше ∠3. Тогда ∠2 = ________________

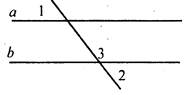
В6. На рисунке прямые а и b параллельны, ∠1 = 80°, ∠3 = 50°. Тогда ∠2 = ________________

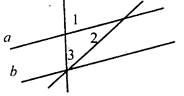
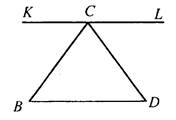
В7. На рисунке через вершину С треугольника BCD проведена прямая KL, параллельная стороне треугольника BD. При этом ∠BCK = 56°, ∠DCL = 64°. Тогда средним углом треугольника будет угол ________________­___________________

Часть 3

С1. Отрезок DM - биссектриса треугольника CDE. Через точку М проведена прямая, пересекающая сторону DE в точке N так, что DN = MN. Вычислите градусные меры углов треугольника DMN, если ∠CDE = 76°.

Ответы:

Часть 1

А1	А2	А3	А4	А5	А6	А7	А8
в	б	а	г	а	а	г	в

Часть 2

В1	В2	B3	В4	В5	В6	В7
Пересекающимися	3 и 5, 4 и 8	Параллельными	108°	65°	30°	∠C = 60°

Часть 3

С1. Возможный вариант оформления решения задачи.

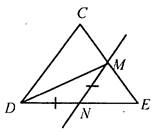
1) DM - биссектриса треугольника, поэтому ∠CDM = ∠MDE = 38°.

2) DN = MN, поэтому треугольник DNMявляется равнобедренным, а значит, ∠MDN = ∠DMN = 38°.

3) Углы DMN и CDM являются накрест лежащими углами при прямых CD и MN и секущей DM, а так как внутренние накрест лежащие углы при прямых CD и MN и секущей DM равны, то прямые DC и MN будут параллельны.

4) Углы CDN и MND являются односторонними при параллельных прямых CD и MN и секущей DE, поэтому сумма углов равна 180°. А значит, ∠DNM = 180° - 76° = 104°.

5) Таким образом, углы треугольника DNM будут равны 104°, 38°, 38°.