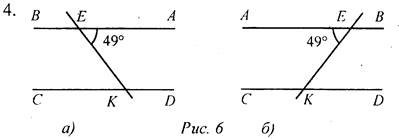РЕШЕНИЕ ЗАДАЧ - Урок 8 - ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

Цель деятельности учителя

Создать условия для подготовки к контрольной работе

Термины и понятия

Параллельные прямые, аксиома, свойства параллельных прямых

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию

Познавательные: осуществляют логические действия.

Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки, осуществляют контроль по результату и способу действия на уровне произвольного внимания и вносят необходимые коррективы.

Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И)

Образовательные ресурсы

• Задания для парной работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Проверить правильность выполнения домашнего задания

(Ф/И)

1. Ответить на вопросы учащихся по домашнему заданию и проверить правильность решения задач.

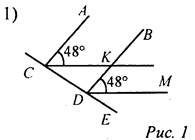
Так как АС || BD, СК || DM, то ∠ACK = ∠BDM = 48°. ∠CDK + ∠EDM = 180° - ∠BDM.

∠CDK в 3 раза больше ∠EDM, тогда 3∠EDM + ∠EDM = 180° - 48°, 4∠EDM = 132°, ∠EDM = 33°.

Тогда ∠KDE = 48° + 33° = 81°.

Ответ: ∠КDЕ = 81°.

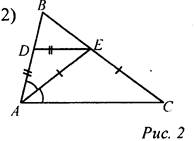
AD = DE, тогда ∠DAE = ∠DEA. АС - биссектриса ΔАВС, тогда ∠DAE = ∠EAC, значит, ∠EAC = ∠DEA, следовательно, DE || АС.

ΔAEC - равнобедренный (АЕ = ЕС), тогда ∠EAC = ∠ACE = 37°, следовательно, ∠DAC = 74°.

DE || АС, ∠DAC = 74°, тогда ∠BDE = 74°.

Ответ: ∠BDE = 74°.

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

(П)

Предлагает учащимся решить пробный вариант контрольной работы.

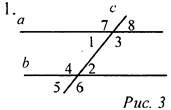
Дано: ∠1 + ∠2 = 88°, а || b.

Найти: все углы, образовавшиеся, при пересечении прямых а и b и секущей с.

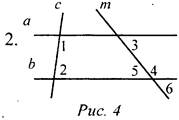
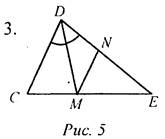
Дано: ∠1 + ∠2 = 180°, ∠3 = 48°.

Найти: ∠4, ∠5, ∠6.

3. Отрезок DM - биссектриса ΔCDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DNM, если ∠CDE = 68°.

4. Прямая ЕК является секущей для АВ и CD (Е ∈ АВ, К ∈ CD). ∠AEK = 49°. При какой величине ∠CKE прямые АВ и CD могут быть параллельными?

1. а || b, тогда ∠1 = ∠2 = 44° (как накрест лежащие углы при параллельных прямых a и b и секущей с); ∠3 = ∠4 (как накрест лежащие); ∠1 = ∠3 - смежные, следовательно, ∠3 = ∠4 = 180° - 44° = 136°; ∠5 = ∠2 = 44° (как вертикальные), ∠4 = ∠6 = 136° (как вертикальные), ∠1 = ∠8 = 44° (как вертикальные), ∠3 = ∠7 = 136°.

2. ∠1 и ∠2 - внутренние односторонние углы и по условию ∠1 + ∠2 = 180°, тогда а || b (по признаку), следовательно, ∠3 = ∠5 = 48° (как внутри накрест лежащие углы), ∠5 = ∠6 (вертикальные), следовательно, ∠3 = ∠5 = ∠6 = 48°, a ∠3 + ∠4 = 180° (односторонние), тогда ∠4 = 132°.

DM - биссектриса ΔCDE, ∠CDE = 68°, тогда ∠CDM = ∠MDN = 34°. CD || MN, тогда ∠DMN = ∠CDM = 34°.

CD || MN, тогда ∠NDC + ∠DNM = 180°.

Значит, ∠DNM = 180° - ∠NDC = 112°.

Ответ: ∠NDM - ∠NMD = 34°, ∠DNM = 112°.

Возможны два случая:

а) ∠AEK = ∠CKE, ∠CKE = 49°, так как AB || CD.

б) ∠AEK + ∠CKE = 180°, так как АВ || CD, тогда ∠CKE = 131°

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

(И) Домашнее задание: повторить теоретический материал, подготовиться к контрольной работе