СУММА УГЛОВ ТРЕУГОЛЬНИКА - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

Цель деятельности учителя

Создать условия для доказательства теоремы о сумме углов треугольника, следствия из нее; для введения понятий остроугольного, прямоугольного и тупоугольного треугольников; для рассмотрения задачи на применение доказанных утверждений

Термины и понятия

Треугольник, противолежащий угол, противолежащая сторона, прилежащий угол и сторона, остроугольный треугольник, тупоугольный, прямоугольный треугольник

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий

Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев; умеют отличать гипотезу от факта.

Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки.

Коммуникативные: умеют работать в сотрудничестве с учителем.

Личностные: проявляют критичность мышления

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные ресурсы

• Чертежи к задачам

I этап. Анализ результатов контрольной работы

Цель деятельности

Совместная деятельность

Проанализировать и откорректировать ошибки, допущенные в контрольной работе

(Ф/И)

1. Проанализировать характерные ошибки, допущенные в контрольной работе.

2. Выполнить работу над ошибками

II этап. Учебно-познавательная деятельность

Цель деятельности

Постановка учебной задачи

Подготовить к восприятию нового материала

(И)

Решение задач по готовым чертежам.

Учащимся дается 2-3 минуты на обдумывание, а затем обсуждаются возможные варианты решений.

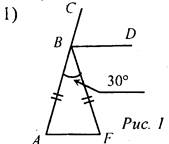
Дано: AF || BD, АВ = BF, ∠B = 30°.

Доказать: BD - биссектриса ∠CBF.

Найти: ∠A, ∠F, сумму углов ΔABF.

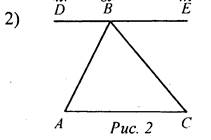
Дано: DE || AC.

Найти: сумму углов ΔАВС.

(Ф)

После решения данных задач учитель задает вопрос, в обсуждении которого должен участвовать весь класс.

- Случайно ли сумма углов треугольника АВС оказалась равной 180°, или этим свойством обладает любой треугольник? (У каждого треугольника сумма углов равна 180°.)

- Это утверждение носит название теоремы о сумме углов треугольника. Итак, тема сегодняшнего урока - “Сумма углов треугольника”

Изучение нового материала

Цель деятельности

Совместная деятельность

Доказать теорему о сумме углов треугольника, рассмотреть следствия, ввести понятия остроугольного, тупоугольного, прямоугольного треугольников

(Ф)

1. Доказательство теоремы о сумме углов треугольника (рис. 125 учебника).

2. Решение задач № 223 (а, б, г), 225, 226 (устно).

3. Перед введением классификации треугольников по углам (п. 31) учащимся задается вопрос: “Может ли треугольник иметь: а) два прямых угла; б) два тупых угла; в) один прямой и один тупой угол?”.

Ответы должны быть обоснованы с помощью теоремы о сумме углов треугольника.

4. Запись в тетрадях вывода из данных ответов (следствие из теоремы о сумме углов треугольника): в любом треугольнике либо все три угла острые, либо два угла острые, а третий - тупой или прямой.

5. Ввести понятия остроугольного, тупоугольного и прямоугольного треугольников и обратить внимание учащихся на названия сторон прямоугольного треугольника - гипотенуза и катет (рис. 126 учебника, модели треугольников)

III этап. Решение задач на закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

При решении простейших задач отработать применение изученной теоремы

(Ф/И)

Организует деятельность учащихся.

1. Решить задачи № 227 и 224 на доске и в тетрадях.

2. Решить задачу № 228 (а, в) на доске и в тетрадях.

3. Решить задачу № 229 на доске и в тетрадях

№ 227.

а) Дано: ΔАВС, АВ = ВС, ∠A > ∠B в 2 раза.

Найти: ∠A, ∠В, ∠C.

Решение:

Примем ∠B = x°, следовательно, ∠A = ∠C= 2х°.

Так как ∠A + ∠B + ∠C = 180°, то 2х + х + 2х = 180°, тогда 5х = 180°, тогда х = 36°.

∠B = 36°, ∠A = ∠C = 72°.

б) Дано: ΔАВС, АВ = ВС, ∠C < ∠BCD в 3 раза.

Найти: ∠A, ∠B, ∠C.

Решение:

Примем ∠C = x°, следовательно, ∠A = х°, ∠BCD = 3х°. Так как ∠BCD = ∠A + ∠B(свойство внешнего угла), то ∠B = 3x - х = 2х. ∠A + ∠B + ∠C = 180°, тогда:

х + 2х + х = 180°,

4x =180°,

х = 45°.

∠A = ∠C = 45°, ∠B = 90°.

№ 224.

Дано: ΔAВС, ∠A : ∠B : ∠C= 2:3:4.

Найти: ∠A, ∠B, ∠C.

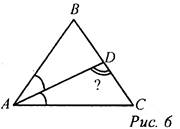
Решение:

Примем 1 часть - x°, следовательно, ∠A = 2х°, ∠B = 3x°, ∠C = 4х°. Так как ∠A + ∠B + ∠C = 180°, то 2х + 3х + 4х = 180, тогда:

9х = 180°,

x = 20°.

20° приходится на 1 часть.

∠A = 2 ∙ 20° = 40°, ∠B = 3 ∙ 20° = 60°, ∠C = 4 ∙ 20° = 80°.

Ответ: 40°, 60°, 80°.

№ 228.

1) Рассмотрим два случая:

а) Угол при основании равен 40°, тогда второй угол при основании равнобедренного треугольника тоже равен 40°; значит, угол при вершине равен 180° - (40° + 40°) = 100°.

б) Угол при вершине равен 40°, тогда углы при основании равны (180° - 40°) : 2 = 70°.

Ответ: 40°, 40°, 100° или 40°, 70°, 70°.

2) Опираемся на доказанное в задаче № 226 утверждение: углы при основании равнобедренного треугольника острые. Значит, угол при вершине равен 100°, а углы при основании равны (180° - 100°): 2 = 40°.

Ответ: 100°, 40° и 40°.

№ 229.

Дано: ΔАВС, АВ = ВС, AD - биссектриса ∠А, ∠C= 50°.

Найти: ∠ADC.

Решение:

1) Так как ΔАВС - равнобедренный, то ∠A= ∠C = 50°.

2) Так как AD - биссектриса ∠A, то ∠BAD= ∠DAC = 25°.

3) Рассмотрим ΔADC:

∠DAC + ∠ADC + ∠C = 180°, тогда:

25° + ∠ADC + 50° = 180°,

∠ADC = 180° - 75°,

∠ADC = 105°.

Ответ: 105°

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что нового узнали на уроке?

- Составьте синквейн к уроку

(И) Домашнее задание: изучить пункты 30-31; ответить на вопросы 1, 3, 4, 5 на с. 89; решить задачи № 223 (в), 228 (б), 230