ПОВТОРЕНИЕ. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ - Урок 2 - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

Цель деятельности учителя	Создать условия для приведения в систему знаний, умений, навыков по теме “Параллельные прямые”; совершенствовать навыки решения задач
Термины и понятия	Параллельные прямые, аксиома параллельности, накрест лежащие углы, соответственные углы, односторонние углы
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют применять изученные понятия, методы для решения задач практического характера		Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют познавательный интерес к изучению предмета
Организация пространства
Формы работы	Фронтальная (Ф); парная (П); индивидуальная (И)
Образовательные ресурсы	• Задания для проверочной работы. • Задания для теста. • Задания для домашней работы
I этап. Актуализация опорных знаний учащихся
Цель деятельности	Задания для проверочной работы
Привести в систему теоретические знания по теме	(И) Проверочная работа на 5-7 минут с взаимопроверкой. Каждое из заданий № 1, 2 оценивается в 4 балла. 1. Укажите номера верных утверждений. 1) Если прямая а параллельна прямой с, а прямая с параллельна прямой b, то прямые а и Ъ параллельны. 2) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. 3) Если точка не лежит на данной прямой, то через нее не всегда можно провести прямую, параллельную данной. 4) Если прямая а перпендикулярна прямой с, а прямая с перпендикулярна прямой b, то прямые а и b пересекаются. 2. По данным рисунка докажите, что прямые с и а параллельны.
II этап. Решение теста
Цель деятельности	Тестовые задания
Совершенствовать навыки решения задач	(П) Решают тест (см. Ресурсный материал), затем проверяют по готовым ответам
III этап. Итоги урока. Рефлексия
Деятельность учителя	Деятельность учащихся
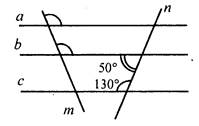
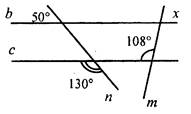
(Ф/И) - Сформулируйте признаки параллельности прямых. - Сформулируйте свойства параллельных прямых. - Оцените свою работу в паре	(И) Домашнее задание. Задание № 1 (оценивается в 4 балла). 1. Прямые а и b параллельны, с - секущая. По данным рисунка найдите все неизвестные углы. Задание № 2 (оценивается в 6 баллов). По данным рисунка найдите х.

Ресурсный материал

Тест

Часть 1

А1. На рисунке секущей является прямая...

а) b;

б) а;

в) с;

г) b или с.

А2. Для угла 4 односторонним будет угол...

а) 1;

б) 8;

в) 5;

г) 3.

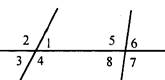
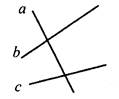
А3. На рисунке углы 1 и 2 являются...

а) односторонними;

б) смежными;

в) накрест лежащими;

г) соответственными.

А4. Дан тупоугольный треугольник АВС с тупым углом В. Через вершину В прямых, параллельных AС, провести...

а) можно бесконечное множество;

б) можно одну;

в) можно две;

г) нельзя ни одной.

А5. На рисунке ∠1 = 112°. Прямые m и n будут параллельными, если ∠2 равен...

а) 68°;

б) 112°;

в) 58°;

г) 68° или 112°.

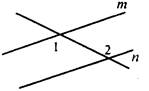
А6. Прямые будут параллельными на рисунке:

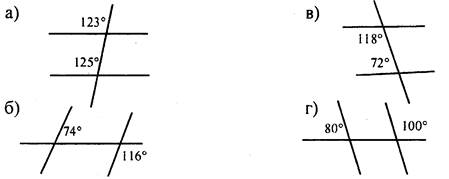
А7. На рисунке прямые m, n, k пересечены секущей р. Параллельными прямыми будут...

а) m и n;

б) m и k;

в) n и k;

г) m, n и k;

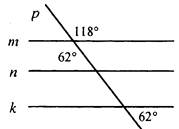
А8. Верным является высказывание:

а) Если при пересечении двух параллельных прямых секущей соответственные углы равны, то прямые параллельны.

б) Если прямая пересекает одну из параллельных прямых, то она перпендикулярна другой.

в) Если две параллельные прямые пересечены секущей, то сумма соответственных углов равна 180°.

г) Если две параллельные прямые пересечены секущей, то однородные углы равны.

Часть 2

В1. Прямые m и n, изображенные на рисунке, являются ____________________________

В2. Из всех углов, изображенных на рисунке, соответственными являются углы ____________________________

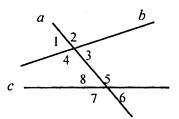
В3. Прямые m и n параллельны. Тогда сумма ∠2 и ∠3 будет равна ____________________________

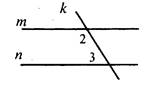
В4. На рисунке прямые m и n - параллельны, ∠3 = 112°. Тогда ∠1 = ____________________________

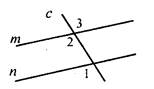
В5. На рисунке m || n, ∠2 на 40° меньше ∠3. Тогда ∠1 = ____________________________

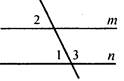
В6. На рисунке прямые c и d — параллельны, ∠2 = 50°, ∠3 = 84°. Тогда ∠1 = ∠ ____________________________

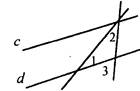
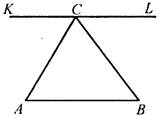
В7. На рисунке через вершину С треугольника АВС проведена прямая KL, параллельная стороне треугольника АВ. При этом ∠ACK = 61°, ∠BCL = 63°. Тогда сумма углов треугольника АВС будет равна ____________________________

Часть 3

С1. Отрезок МР - биссектриса треугольника MNK. Через точку Р проведена прямая, параллельная стороне MN и пересекающая сторону МК в точке Е. Вычислите градусные меры углов треугольника МРЕ, если ∠NMK = 84°.

Ответы:

Часть 1

А1	А2	А3	А4	А5	А6	А7	А8
б	б	в	б	б	г	г	а

Часть 2

В1	В2	В3	В4	В5	В6	В7
Параллельными	3 и 6, 2 и 5, 1 и 8, 4 и 7	180°	68°	70°	34°	180°

Часть 3

Возможный вариант оформления решения задачи. С1.

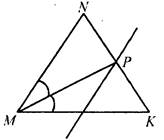
1. ∠MNK и ∠PEMявляются односторонними при параллельных прямых MN и РЕ и секущей МК, поэтому сумма их равна 180°, а значит, ∠PEM = 96°.

2. МР - биссектриса треугольника, поэтому ∠NMP = ∠PMK = 42°.

3. ∠NMP = ∠MPE - накрест лежащие при параллельных прямых MN и РЕ и секущей МР, а так как внутренние накрест лежащие углы при параллельных прямых MN и РЕ равны, то ∠MPE = 42°.

4. Так образом, ∠MPE = ∠EMP = 42°, ∠MEP = 96°.