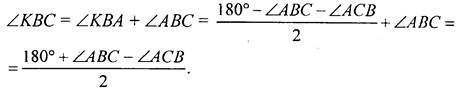Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
ПОВТОРЕНИЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
|
Цель деятельности учителя |
Создать условия для повторения основных задач на построение; совершенствовать навыки решения задач на построение |
|||
|
Термины и понятия |
Построение угла, равного данному, построение биссектрисы угла, построение перпендикулярных прямых, середины отрезка |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют применять изученные понятия, результаты, методы для решения задач практического характера |
Познавательные: умеют планировать и осуществлять деятельность, направленную на решение задач исследовательского характера. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют познавательный интерес к изучению предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для индивидуальной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Повторить основные задачи на построение |
(Ф/И) 1. Шесть учеников выполняют у доски следующие задания: 1) на данном луче от его начала отложить отрезок, равный данному; 2) отложить от данного луча угол, равный данному; 3) построить биссектрису данного неразвернутого угла; 4) построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка; 5) построить середину данного отрезка; 6) построить прямую, проходящую через данную точку и перпендикулярную к прямой, не проходящей через данную точку. 2. Пока учащиеся у доски готовятся, класс выполняет дифференцированные задания. Построить треугольник: 1) по двум сторонам и углу между ними; 2) по стороне и прилежащим к ней углам; 3) по трем сторонам |
|||
|
II этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать навыки решения задач на построение |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 353 на доске и в тетрадях. 2. Решить самостоятельно задачи № 354, 360, 362 (одну задачу решить по полной схеме) |
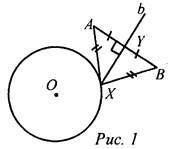
№ 353. Анализ (см. рис. 1):
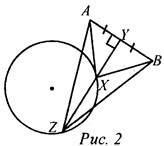
Пусть X - искомая точка, то есть АХ = ХВ, тогда ΔАХВ - равнобедренный и XY - медиана, высота и биссектриса. Отсюда получаем план построения. План построения: 1) Построить точку Y - середину АВ. 2) Построить прямую, проходящую через Y и перпендикулярную АВ. 3) Прямая b пересекается с окружностью в точках Х и Z. X и Z - искомые точки. Построение (см. рис. 2):
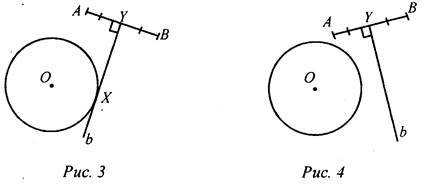
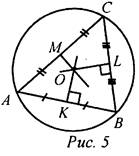
Доказательство: ΔAYX = ΔBYX по двум катетам (они прямоугольные, так как YX ⊥ АВ, AY = YB, так как Y - середина АВ), тогда АХ = ВХ, то есть точка X лежит на данной окружности и равноудалена от концов отрезка АВ. Таким же образом можно доказать, что точка Zудовлетворяет всем условиям задачи. Исследование: Задача может иметь: а) два решения (см. план построения и построение); б) одно решение, если прямая b имеет одну общую точку с окружностью (касается ее) (рис. 3); в) ни одного решения, если прямая b не имеет общих точек с окружностью (рис. 4).
№ 354.
Соединяем точки А, В и С. Находим середины отрезков АВ, ВС и АС, соответственно К, L и М Проводим перпендикуляры (серединные перпендикуляры ΔАВС). Находим точку О - их точку пересечения. Проводим окружность радиуса АО = ВО = СО с центром в точке О. Вокруг треугольника всегда можно описывать окружность, поэтому задача не имеет решения, лишь когда точки лежат на одной прямой. № 360.
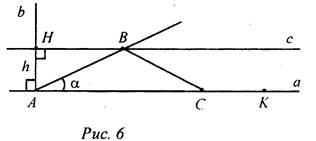
Проводим прямую а. Отмечаем на ней точку А - одну из вершин нашего треугольника, на прямой откладываем отрезок, равный периметру треугольника. На прямой b откладываем отрезок AH, равный высоте треугольника. Строим заданный ∠a с вершиной в точке А. Проводим прямую с ⊥ b, Н ⊥ с. Обозначим точку пересечения с со стороной ∠a - В. От точки К откладываем на прямой а отрезок, равный АВ - КС. Соединяем В и С. АВС - искомый треугольник. № 362.
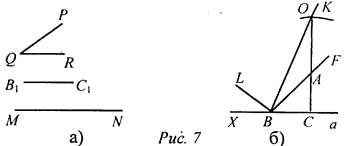
Пусть надо построить ΔАВС, и даны ∠PQR и отрезки В1С1, равный стороне треугольника, и MN, равный сумме двух других сторон треугольника (см. рис. а). Проведем произвольную прямую а, отметим на ней точку В и точку X (см. рис. б). От луча ВХ отложим угол XBL, равный углу PQR (см. пункт 23учебника). От точки В отложим отрезок, равный данному отрезку В1С1. Построим биссектрису ВК угла LBC (см. пункт 23учебника). Построим окружность С радиусом, равным MN, и центром С, она пересечет луч ВК в точке О. Отложим от луча ВК ∠KBF, равный углу ВКС. Луч BF пересечет СО в точке A. Треугольник АВС - искомый, докажем это. ∠KAB = ∠ABC + ∠ACB (как внешний). ΔКАВ - равнобедренный (так как ∠BKA = ∠KBA по построению). Значит,
АВ = АК, так как ΔКВА - равнобедренный, значит, MN = КА + АС = АВ + АС, следовательно, наши построения верны |
||
|
III этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - Какой этап в задачах на построение у вас вызывает наибольшее затруднение? - Оцените свою работу на уроке |
(И) Домашнее задание: решить задачи № 352, 356, 361 (одну задачу решить по полной схеме) |
|||