Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
СОВМЕСТНЫЕ ДЕЙСТВИЯ С РАЦИОНАЛЬНЫМИ ДРОБЯМИ - Урок 2 - РАЦИОНАЛЬНЫЕ ДРОБИ
Цель: продолжить формирование умения выполнять преобразования на совместные действия с дробями.
Ход урока
I. Организационный момент.
II. Устная работа.
Вычислите:
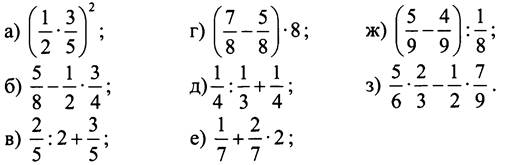
III. Формирование умений и навыков.
• Выполнение заданий по учебнику: № 154 (а, в), 155, 159, 161.
№ 155.
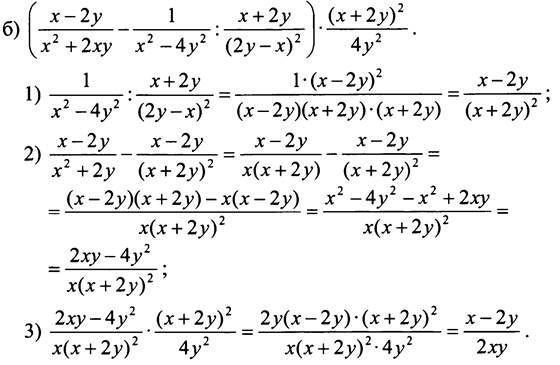
№ 161.
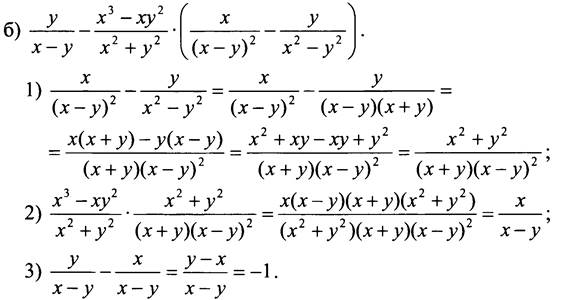
Таким образом, исходное выражение принимает значение -1 при любых значениях переменных х и у.
• Дополнительные задания (для учащихся с высоким уровнем подготовки).
№ 157.
Сначала упростим данное выражение:
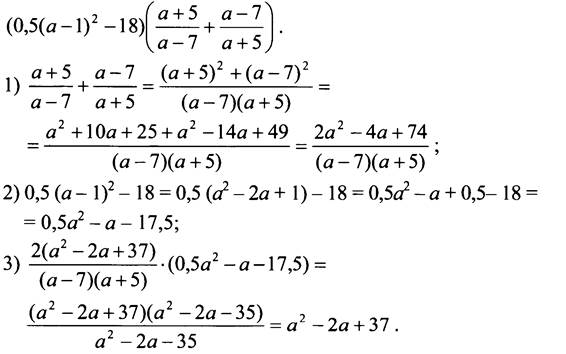
Представим полученный многочлен в виде суммы квадрата двучлена и некоторого числа:
![]()
Поскольку выражение (а - 1)2 неотрицательно при любом а, то выражение (а - 1)2 + 36 принимает наименьшее значение при а = 1, и это значение равно 36.
Ответ: 36.
№ 160.
![]()
Преобразуем выражение, стоящее в левой части равенства:
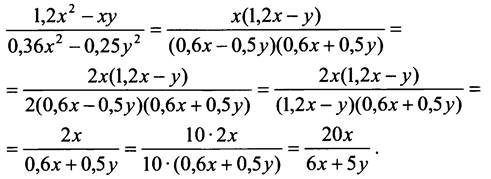
Таким образом, эти выражения тождественно равны.
• Задания на карточках для сильных учащихся.
Карточка 1
Упростите выражение:
![]()
Решение
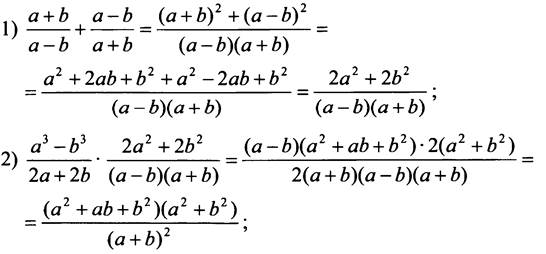

Карточка 2
Упростите выражение:
![]()
Решение
Данное выражение лучше преобразовать “цепочкой”, при этом рациональнее будет сначала раскрыть скобки:
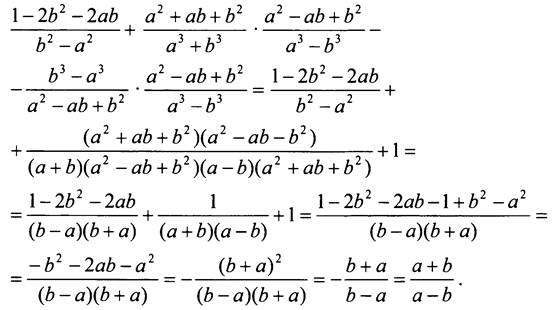
IV. Итоги урока.
- Как выполнить сложение или вычитание рациональных дробей? Сформулируйте правила умножения и деления рациональных дробей.
- Какими способами можно упрощать выражения, содержащие совместные действия с дробями?
Домашнее задание: № 154 (б, г), 156, 162; № 158, 160 (б) (дополнительно).