НАХОЖДЕНИЕ СРЕДНЕГО ГАРМОНИЧЕСКОГО РЯДА ПОЛОЖИТЕЛЬНЫХ ЧИСЕЛ - РАЦИОНАЛЬНЫЕ ДРОБИ

Цели: формировать умение отыскивать среднее гармоническое для ряда положительных чисел; продолжить формирование умения выполнять преобразования дробных выражений.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Вычислите:

2. Найдите среднее арифметическое чисел:

III. Объяснение нового материала.

Рассмотрим задачу на вычисление средней скорости, в которой данные будут числовыми.

Задача. Одну и ту же дистанцию лыжник прошёл сначала со скоростью 18 км/ч, а затем — со скоростью 20 км/ч. Какова была средняя скорость на всём пути?

Очень часто учащиеся допускают ошибку: находят среднюю скорость как среднее арифметическое данных скоростей. Так отыскивать среднюю скорость нельзя. Чтобы найти среднюю скорость, нужно разделить весь пройденный путь на общее время движения на этом пути. Если обозначить длину дистанции как S км, то в первый раз лыжник потратил на её прохождение S/18 ч, а во второй раз S/20 ч. Получим: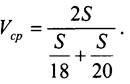

Упростим полученное дробное выражение:

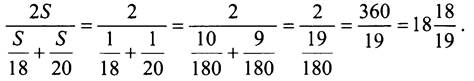
Таким образом, средняя скорость лыжника на всём пути была равна

Рассмотрим пример 4 из учебника, в котором показан общий вид решения подобных задач. Объясните понятие среднего гармонического ряда положительных чисел.

IV. Формирование умений и навыков.

Все задания можно разбить на две группы:

1-я группа. Задачи на нахождение среднего гармонического ряда положительных чисел: № 170 (а, в), 171, 172, 173.

2-я группа. Задания на преобразование дробных выражений: № 247, 248 (а, в), 249 (б).

• Выполнение заданий по учебнику.

№ 247.

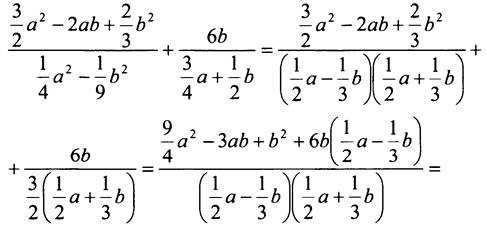
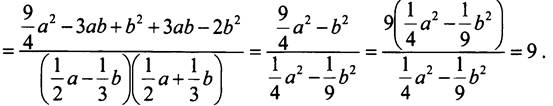
Таким образом, исходное выражение не зависит от значений а и b.

№ 249.

б) Чтобы выражение 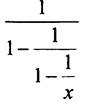имело смысл, необходимо выполнение трёх условий:

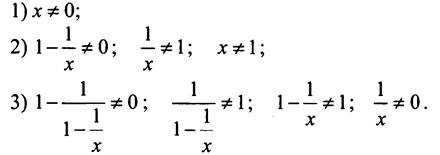
Ответ: x ≠ 0; x ≠ 1.

V. Итоги урока.

- Сформулируйте правила действий с дробными выражениями. Как найти среднюю скорость движения на определённом участке пути?

- По какой формуле вычисляется среднее гармоническое ряда положительных чисел а₁, a₂, ..., a_n?

Домашнее задание: № 170 (б), 250, 251, 248 (б, г).