КОНТРОЛЬНАЯ РАБОТА 2 - РАЦИОНАЛЬНЫЕ ДРОБИ

Вариант 1

1. Представьте в виде дроби:

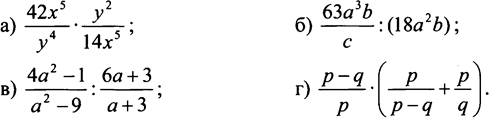
2. Постройте график функции у = 6/x. Какова область определения функции? При каких значениях х функция принимает отрицательные значения?

3. Докажите, что при всех значениях b ≠ ±1 значение выражения не зависит от b.

4. При каких значениях а имеет смысл выражение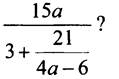

Вариант 2

1. Представьте в виде дроби:

2. Постройте график функции у = -6/x. Какова область определения функции? При каких значениях х функция принимает положительные значения?

3. Докажите, что при всех значениях x ≠ ±2 значение выражения не зависит от х.

4. При каких значениях b имеет смысл выражение

Вариант 3

1. Представьте в виде дроби:

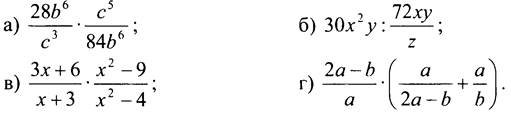
2. Постройте график функции у = 4/x. Какова область определения функции? При каких значениях х функция принимает положительные значения?

3. Докажите, что при всех значениях у ≠ ±3 значение выражения 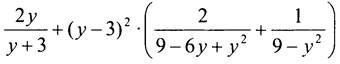не зависит от у.

4. При каких значениях х имеет смысл выражение

Вариант 4

1. Представьте в виде дроби:

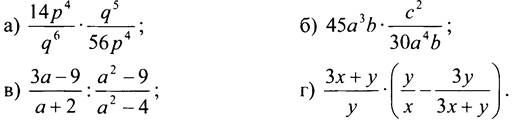
2. Постройте график функции у = -4/x. Какова область определения функции? При каких значениях х функция принимает отрицательные значения?

3. Докажите, что при всех значениях а ≠ ±5 значение выражения не зависит от а.

4. При каких значениях y имеет смысл выражение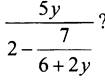

Решение вариантов контрольной работы

Вариант 1

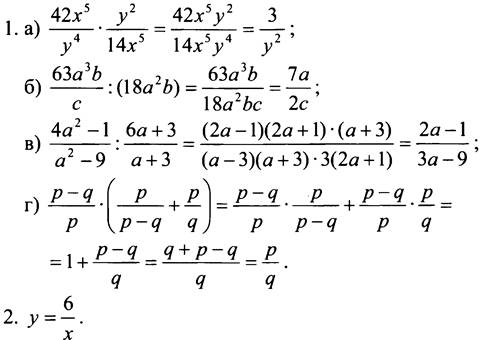
x	1	2	3	6	- 1	-2	-3	-6
y	6	3	2	1	-6	-3	-2	- 1

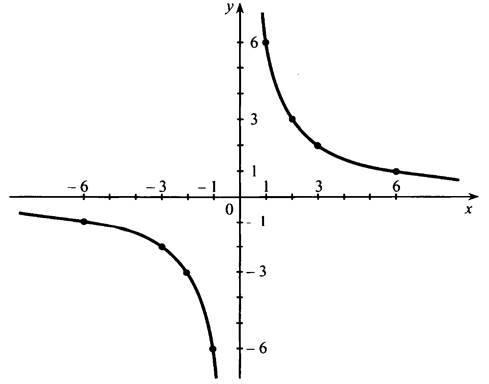
Область определения функции: (-∞; 0) и (0; +∞).

Функция принимает отрицательные значения при х є (-∞; 0).

3. Упростим данное выражение:

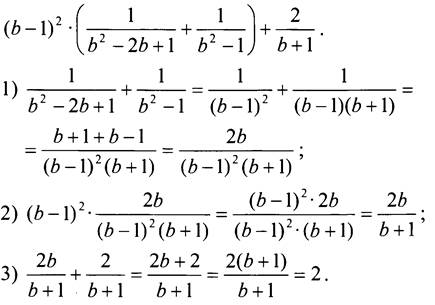
Таким образом, при любом значении b данное выражение равно 2, то есть не зависит от b.

4. Чтобы выражение имело смысл, должны выполняться два условия:

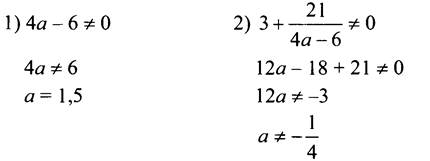
Ответ: a ≠ 1,5; a ≠ -1/4.

Вариант 2

x	1	2	3	6	- 1	-2	-3	-6
y	-6	-3	-2	- 1	6	3	2	1

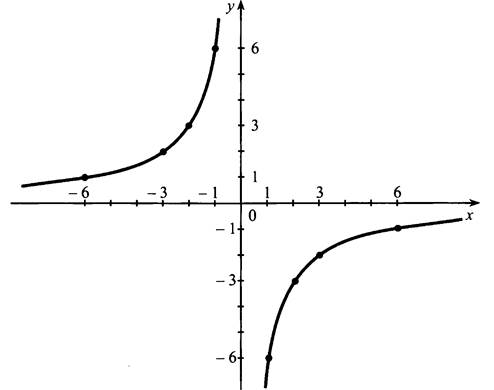
Область определения функции: (-∞; 0) и (0; +∞).

Функция принимает положительные значения при x є (-∞; 0).

3. Упростим данное выражение:

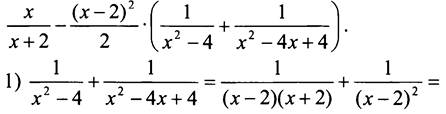
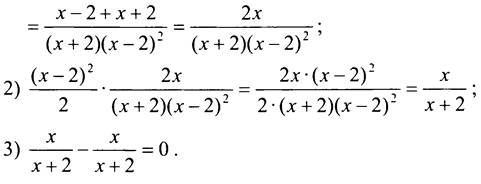
Таким образом, при любом значении х данное выражение равно нулю, то есть не зависит от х.

4. Чтобы выражение 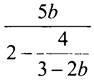имело смысл, должны выполниться два условия:

Ответ: b ≠ 0,5; b ≠ 1,5.

Вариант 3

x	1	2	4	- 1	-2	-4
y	4	2	1	-4	-2	- 1

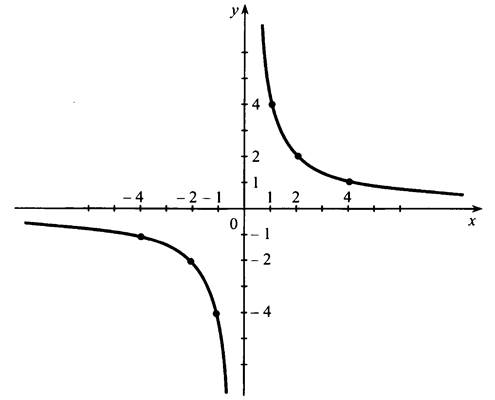
Область определения функции: (-∞; 0) и (0; +∞).

Функция принимает положительные значения при х є (0; +∞).

3. Упростим выражение:

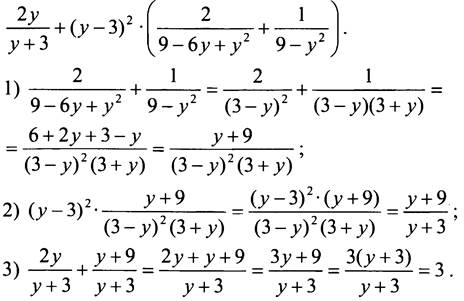
Таким образом, при любом значении у данное выражение равно 3, то есть не зависит от y.

4. Чтобы выражение 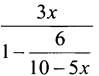имело смысл, должны выполняться два условия:

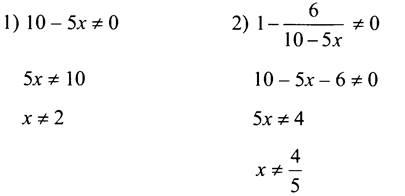
Ответ: х ≠ 2; х ≠ 4/5.

Вариант 4

x	1	2	4	- 1	-2	-4
y	-4	-2	- 1	4	2	1

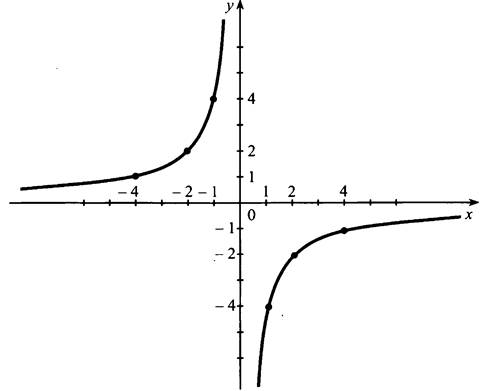
Область определения функции: (-∞; 0) и (0; +∞).

Функция принимает отрицательные значения при х є (0; +∞).

3. Упростим данное выражение:

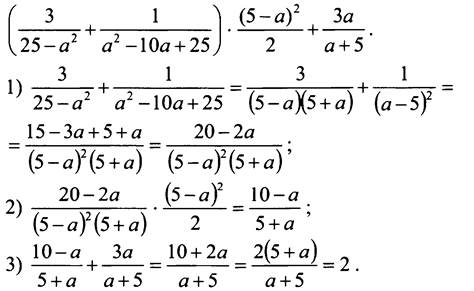
Таким образом, при любом значении a данное выражение равно 2, то есть не зависит от a.

4. Чтобы выражение 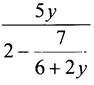имело смысл, должны выполняться два условия:

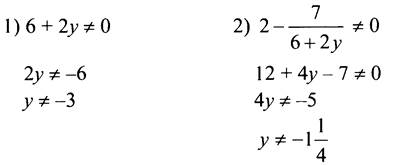
Ответ: