ПРЕДСТАВЛЕНИЕ ДРОБИ В ВИДЕ СУММЫ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ

Цели: изучить метод неопределённых коэффициентов; формировать умение представлять рациональную дробь в виде суммы дробей.

Ход урока

I. Изучение нового материала.

Существуют задачи, в которых нужно уметь выполнять действие, обратное сложению дробей: представлять рациональную дробь в виде суммы дробей.

Разберем три основных приёма, позволяющих совершить данное действие.

1-й приём. Использование элементарных преобразований

2-й приём. Деление уголком числителя на знаменатель (пример 3 из учебника).

3-й приём. Метод неопределённых коэффициентов (пример 1 из учебника).

II. Формирование умений и навыков.

1. № 197, 198, 199 - использование метода неопределённых коэффициентов.

2. № 200, 201, 203 - выделение целой части из дроби путём деления числителя на знаменатель.

3. № 202, 204 - выделение целой части из дроби с помощью элементарных преобразований.

4. № 205, 206, 207.

• Выполнение заданий.

№ 205.

Известно, что Необходимо найти все пары натуральных чисел, удовлетворяющих этому уравнению.

Выразим из этого уравнения переменную а через b:

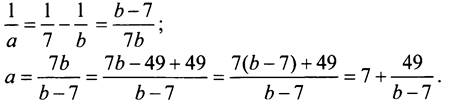
Значение дроби является натуральным числом в трех случаях:

Ответ: (56; 8), (14; 14), (8; 56).

№ 206.

Известно, что Преобразуем выражение, стоящее в левой части равенства:

Таким образом, теперь нам известно значение выражения x/y. Выделим целую часть из данной в условии дроби.

Подставляя в это выражение значение x/y = 3, получим: 3 ∙ 3² - 3 + 6 = 30.

Ответ: 30.