ВЫЧИСЛЕНИЕ КВАДРАТНОГО КОРНЯ ИЗ ПРОИЗВЕДЕНИЯ И ДРОБИ - КВАДРАТНЫЕ КОРНИ

Цели: выявить и доказать свойства квадратного корня; формировать умение непосредственно применять их при вычислениях.

Ход урока

I. Организационный момент.

II. Устная работа.

Вычислите:

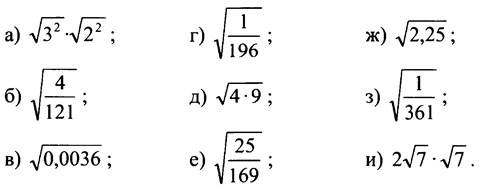
III. Объяснение нового материала.

При объяснении необходимо показать преимущество, которое дает при вычислениях использование свойств корней.

Задание: вычислите на калькуляторе значения нескольких корней:

- Вычислите другим способом - без использования калькулятора:

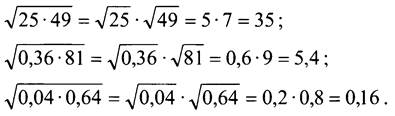
Сравните результаты и выдвиньте предположения. (Такой прием будет справедлив для любых неотрицательных чисел.)

Сформулируйте данное свойство.

Учитель четко сам формулирует свойство: корень из произведения неотрицательных чисел равен произведению корней из этих чисел.

Проводится доказательство свойства (выносится на доску):

Аналогично формулируется второе свойство (выносится на доску):

Вычислите √2 ∙ √8. (Большинство учащихся догадается внести множители под общий корень.)

Использование полученных равенств справа налево дает правила умножения и деления корней:

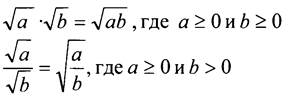
IV. Формирование умений и навыков.

На этом уроке основное внимание следует уделить непосредственному применению изученных свойств квадратных корней при вычислениях.

• № 369, 370, 378, 379.

• № 382, 383, 385 (а, в, д, ж), 386.

V. Итоги урока.

- Сформулируйте свойство вычисления корня из произведения неотрицательных чисел.

- Сформулируйте свойство вычисления корня из частного от деления неотрицательного числа на положительное число.

- Сформулируйте правила умножения и деления корней.

- Как вычислить корень из смешанного числа?

Домашнее задание: № 371, 384, 385 (б, г, е, з).