КВАДРАТНЫЙ КОРЕНЬ ИЗ ПРОИЗВЕДЕНИЯ И ДРОБИ ПРИ ПРЕОБРАЗОВАНИИ ВЫРАЖЕНИЙ С КОРНЕМ - КВАДРАТНЫЕ КОРНИ

Цель: продолжить формирование умения применять свойства квадратного корня при преобразовании выражений.

Ход урока

I. Организационный момент.

II. Устная работа.

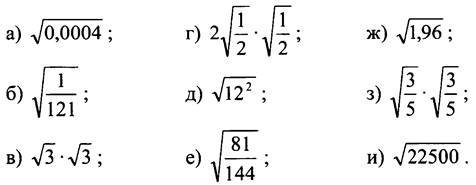
III. Формирование умений и навыков.

• Выполнение заданий № 372, 387 (а, в, д, ж), 374, 376, 380.

№ 374.

Это задание может вызвать затруднения у учащихся. Раньше им встречались выражения вида √аb, в которых √а и √b извлекались. При выполнении предложенного задания это свойство корней напрямую применять нецелесообразно.

Необходимо подкоренное выражение представить в виде произведения таких множителей, из которых корень извлекается.

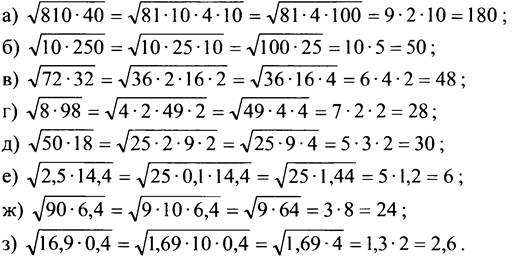
№ 376.

Учащиеся довольно часто допускают следующую ошибку:

В этом случае следует предложить им вычислить значение подкоренного выражения, извлечь корень и сравнить полученные результаты.

Данный пример помогает избежать подобных ошибок в дальнейшем и еще раз заостряет внимание учащихся на свойствах квадратных корней.

Если в примерах а) и б) учащиеся просто могут вычислить значение подкоренного выражения и извлечь корень, то в следующих примерах это можно сделать только при помощи калькулятора. Чтобы учащиеся “увидели” формулу разности квадратов, нужно требовать вычислений без калькулятора.

№ 380.

Преобразуем выражение, стоящее в правой части равенства:

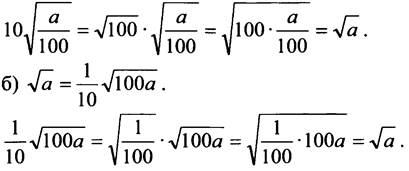
• Задания на карточках для сильных учащихся.

Карточка 1

1. Расположите в порядке возрастания числа:

2. Найдите значение выражения:

3. Известно, что а < 0 и b < 0. Представьте выражение √аb в виде произведения корней.

Карточка 2

1. Расположите в порядке возрастания числа:

2. Найдите значение выражения:

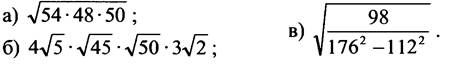
3. Известно, что а < 0 и b < 0. Представьте выражение в виде частного корней.

Решение заданий карточки 1

1. Все дроби имеют числители, равные 1. Поэтому достаточно сравнить знаменатели дробей. Имеем:

поэтому

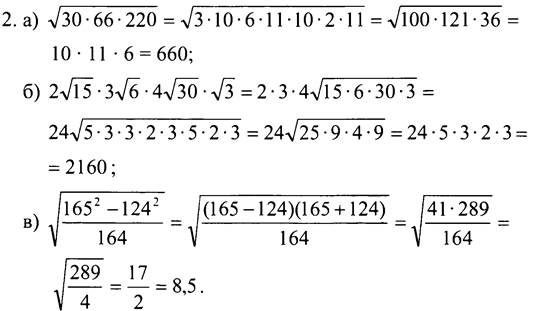
3. Если a < 0 и b < 0, то

Чтобы подкоренные выражения стали положительными, перед ними нужно поставить “минус”. Получим, что

IV. Итоги урока.

- Сформулируйте свойство вычисления корня из произведения неотрицательных чисел.

- Сформулируйте свойство вычисления корня из частного от деления неотрицательного числа на положительное число.

- Сформулируйте правила умножения и деления корней.

- Как преобразовать выражение вида √xy, если корни из чисел х и у не извлекаются?

Домашнее задание: № 373, 375, 377 (б, г, е), 387 (б, г, е, з).