КВАДРАТНЫЙ КОРЕНЬ ИЗ С ТЕПЕНИ ПРИ ПРЕОБРАЗОВАНИИ РАЗЛИЧНЫХ ВЫРАЖЕНИЙ - КВАДРАТНЫЕ КОРНИ

Цель: продолжить формирование умения применять свойство квадратного корня из степени.

Ход урока

I. Организационный момент.

II. Устная работа.

Вычислите:

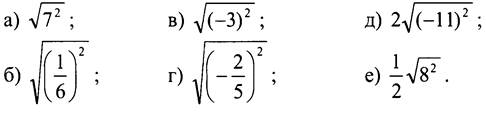
III. Формирование умений и навыков.

Все задания можно условно разбить на две группы.

1-я группа. Задания, в которых необходимо применить формулу раскрыв знак модуля в зависимости от значения х: № 395, 396 (а, б, г, д, ж), 484 (устно), 487 (а, б, г, ж).

№ 487.

Так как а² ≥ 0 при любом а и b² ≥ 0 при любом b, то Имеем:

По условию b ≥ 0, значит, при любом с, значит, Имеем:

По условию р ≥ 0, поэтому поэтому Имеем:

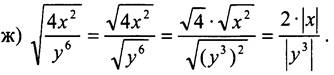
По условию x < 0, поэтому |x| = -х; у < 0, поэтому Имеем: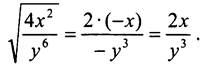

2-я группа. Задания повышенного уровня сложности:

- Упростите выражение:

№ 397.

Если 0 ≤ a < 2, то a - 2 < 0, то есть

Если a ≥ 2, то a - 2 ≥ 0, то есть

№ 400.

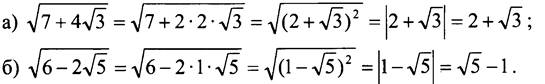
№ 485.

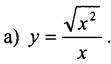
Преобразовав выражение получим функцию Для построения её графика нужно раскрыть знак модуля, рас смотрев два случая:

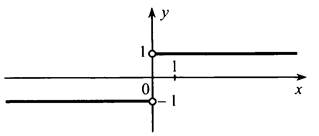
1) если х > 0, то то есть у = 1;

2) если х < 0, то то есть у = -1.

Получим такой график:

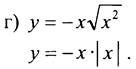
1) если х ≥ 0, то у = -х²;

2) если х < 0, то у = х².

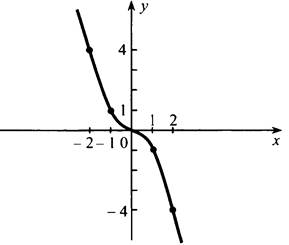
№ 488.

Преобразуем выражение, стоящее под корнем. Сначала перемножим первый множитель с четвёртым, а второй - с третьим.

Сделаем замену: n² + 3n = m. Получим:

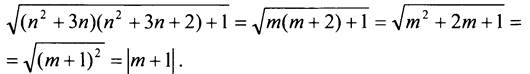
Если n - натуральное число, то выражение n² + 3n принимает натуральные значения, то есть число m - натуральное. Это значит, что |m + 1| = m + 1 и это выражение принимает всегда натуральные значения.

IV. Проверочная работа.

Вариант 1

1. Вычислите:

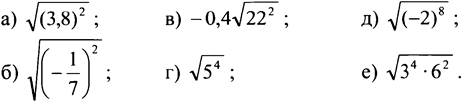
2. Упростите выражение:

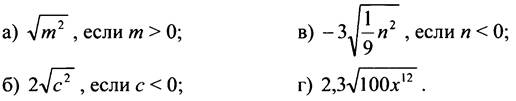
3.* Вычислите:

Вариант 2

1. Вычислите:

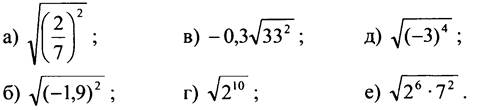
2. Упростите выражение:

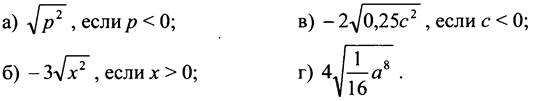
3.* Вычислите:

V. Итоги урока.

- Чему равно выражение √x², если x > 0? x < 0?

- При каких значениях а верно равенство

- Может ли выражение √a⁴ принимать отрицательные значения? Почему?

- Какие значения может принимать выражение √у¹⁴?

Домашнее задание: № 396 (в, е, з), 487 (в, д, е, з); № 398, 485 (б, в) (дополнительно).