КОНТРОЛЬНАЯ РАБОТА 3 - КВАДРАТНЫЕ КОРНИ

Вариант 1

1. Вычислите:

2. Найдите значение выражения:

3. Решите уравнение: а) х² = 0,49; б) х² = 10.

4. Упростите выражение:

5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число √17.

6. При каких значениях переменной а имеет смысл выражение

Вариант 2

1. Вычислите:

2. Найдите значение выражения:

3. Решите уравнение: а) х² = 0,64; б) х² = 17.

4. Упростите выражение:

5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число √38.

6. При каких значениях переменной х имеет смысл выражение

Вариант 3

1. Вычислите:

2. Найдите значение выражения:

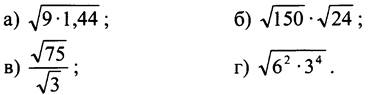
3. Решите уравнение: а) х² = 0,81; б) х² = 46.

4. Упростите выражение:

5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число √28.

6. При каких значениях переменной х имеет смысл выражение

Вариант 4

1. Вычислите:

2. Найдите значение выражения:

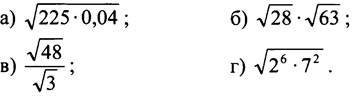
3. Решите уравнение: а) х² = 0,09; б) х² = 92.

4. Упростите выражение:

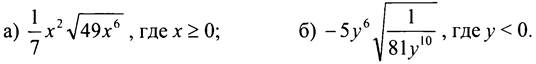
5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число √56.

6. При каких значениях переменной у имеет смысл выражение

Решение вариантов контрольной работы

Вариант 1

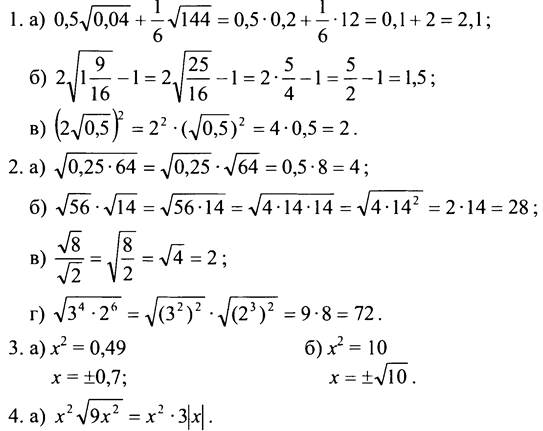
Так как х ≥ 0, то |x| = х. Получим:

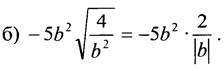
Так как b < 0, то |b| = -b. Получим:

6. Чтобы выражение имело смысл, должны выполняться два условия:

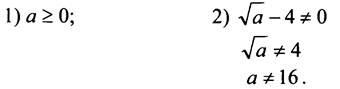
Ответ: а ≥ 0 и а ≠ 16.

Вариант 2

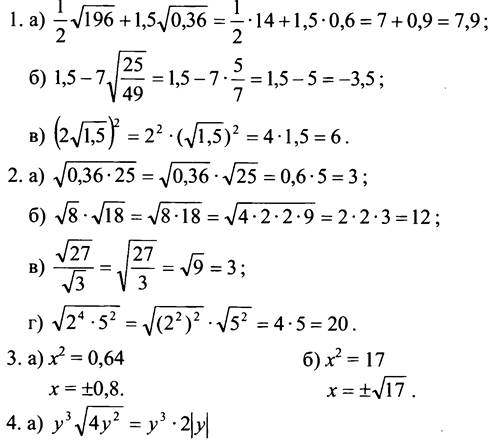
Так как у ≥ 0, то |у| = у. Получим:

Так как a < 0, то |а| = -а. Получим: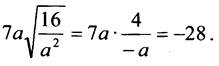

6. Чтобы выражение имело смысл, должны выполняться два условия:

Ответ: х ≥ 0 и х ≠ 25.

Вариант 3

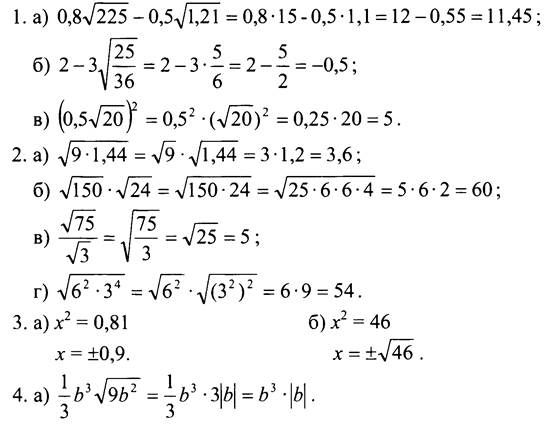
Так как b ≤ 0, то |b| = -b. Получим:

Так как х > 0, то |х| = х . Получим:

6. Чтобы выражение имело смысл, должны выполняться два условия:

Ответ: х ≥ 0 и х ≠ 4.

Вариант 4

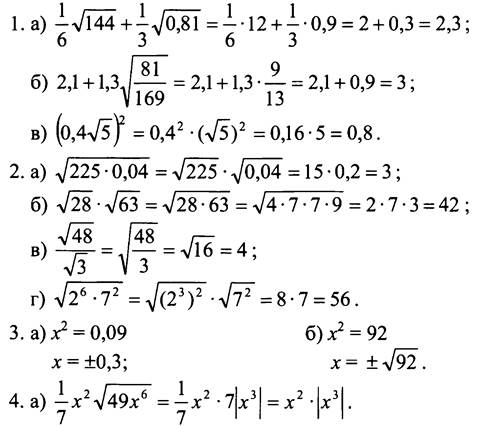
Так как x ≥ 0, то |х³| = х³. Получим:

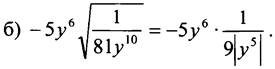
Так как у < 0, то |y⁵| = -y⁵. Получим: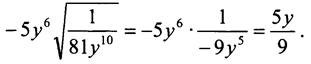

6. Чтобы выражение имело смысл, должны выполняться два условия:

Ответ: у ≥ 0.