ВЫНЕСЕНИЕ МНОЖИТЕЛЯ ЗА ЗНАК КОРНЯ. ВНЕСЕНИЕ МНОЖИТЕЛЯ ПОД ЗНАК КОРНЯ - КВАДРАТНЫЕ КОРНИ

Цели: изучить такие преобразования квадратных корней, как вынесение множителя за знак корня и внесение множителя под знак корня; формировать умение выполнять эти преобразования.

Ход урока

I. Организационный момент.

II. Устная работа.

Вычислите:

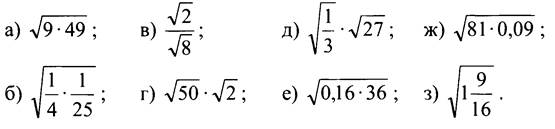
III. Объяснение нового материала по учебнику.

Объяснению материала следует придать больше проблемности и требовать от учащихся самостоятельности при формулировании выводов.

1. Поставить проблему: как сравнить значения выражений √50 и 6√2.

2. Рассмотреть два способа, которые могут быть использованы для этого.

3. Сделать выводы.

- Какое действие нужно было выполнить при решении задачи первым способом? (Такое преобразование называется вынесением множителя из-под знака корня.)

Аналогично проанализируем действие, выполняемое при решении задачи вторым способом. Это преобразование называется внесением множителя под знак корня.

- В каких случаях пригодится умение выносить множитель из-под знака корня и вносить множитель под знак корня?

Выделите две основные ситуации, в которых применяются данные умения:

1) Сравнение двух выражений.

2) Преобразование выражений.

IV. Формирование умений и навыков.

Задания можно разбить на три группы:

1-я группа. Вынесение множителя за знак корня: № 407, 408.

Не все учащиеся могут быстро раскладывать подкоренные выражения на два “удобных” множителя. Некоторые подбирают “очевидные” делители, например 4 или 9. В этом случае не нужно требовать от учащихся, чтобы они отыскивали другое разложение, главное - получение верного результата.

Например,

Этот же результат можно получить по-другому:

2-я группа. Внесение множителя под знак корня: № 410, 412.

При выполнении задания № 412 учащиеся могут допустить довольно распространённую ошибку: внести под корень отрицательный множитель:

В этом случае нужно предложить учащимся сравнить с нулем данное и полученное число. Данное число является отрицательным, а после внесения множителя под корень получили положительное число. Учащиеся должны найти ошибку в рассуждениях и сделать вывод.

3-я группа. Сравнение значений выражений с корнями: № 411, 414, 416, 417.

№ 411.

Из данных четырех выражений не имеет смысла то, которое содержит под корнем отрицательное число. Таким образом, нужно сравнить с нулем все подкоренные выражения. А для этого нужно сравнить уменьшаемое и вычитаемое.

1) имеет смысл, так как 2√17 > 4.

2) имеет смысл, так как 2√2 > √7.

3) имеет смысл, так как 6√3 > 7√2.

4) не имеет смысла, так как 8√3 < 14.

V. Итоги урока.

- В чем состоит прием вынесения множителя из-под знака корня; внесения множителя под знак корня?

- Как сравнить значения выражений, содержащих корни?

- Как сравнить корень с целым числом?

Домашнее задание: № 409, 413, 415.