СОКРАЩЕНИЕ ДРОБЕЙ, СОДЕРЖАЩИХ КВАДРАТНЫЕ КОРНИ, И ОСВОБОЖДЕНИЕ ОТ ИРРАЦИОНАЛЬНОСТИ В ЗНАМЕНАТЕЛЕ ДРОБИ - КВАДРАТНЫЕ КОРНИ

Цель: продолжить формирование умения преобразовывать выражения, содержащие квадратные корни.

Ход урока

I. Организационный момент.

II. Устная работа.

Приведите подобные радикалы:

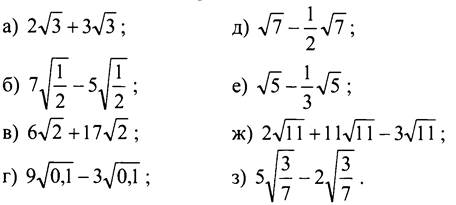
III. Формирование умений и навыков.

• Задания можно разбить на две группы:

1-я группа. Сокращение дробей, содержащих квадратные корни: № 427, 428, 429.

2-я группа. Освобождение от иррациональности в знаменателе дроби: № 431, 433 (а, в, д).

№ 433.

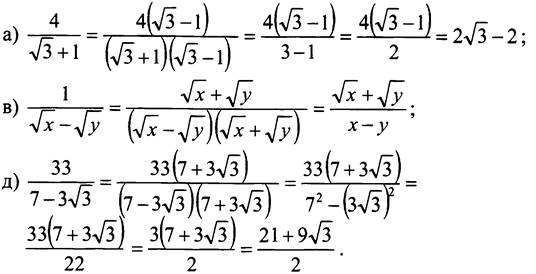
• Дополнительные задания для учащихся с высоким уровнем подготовки.

1) Сократите дробь:

Решение

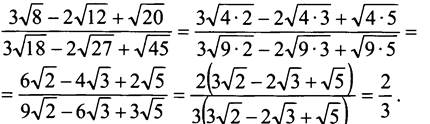
2) Вычислите:

Решение

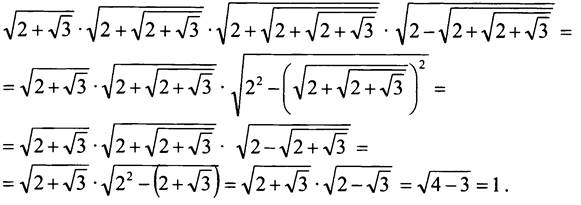
3) Освободитесь от иррациональности в знаменателе дроби:

Решение

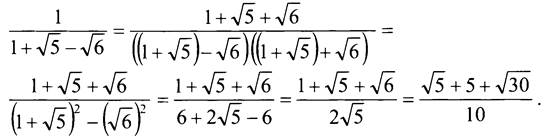
IV. Проверочная работа.

Вариант 1

1. Упростите выражение:

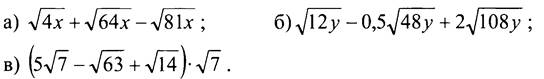
2. Выполните действия:

3. Сократите дробь:

4. Освободитесь от иррациональности в знаменателе дроби:

Вариант 2

1. Упростите выражение:

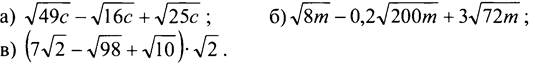
2. Выполните действия:

3. Сократите дробь:

4. Освободитесь от иррациональности в знаменателе дроби:

V. Итоги урока.

- Как приводить подобные радикалы?

- Как освобождаться от иррациональности в знаменателе дроби в различных случаях?

Домашнее задание: № 430, 432, 433 (б, г, е), № 503 (а, д), 507 (а) (дополнительно).