КОНТРОЛЬНАЯ РАБОТА 4 - КВАДРАТНЫЕ КОРНИ

Вариант 1

1. Упростите выражение:

2. Сравните: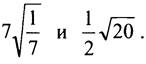

3. Сократите дробь:

4. Освободите дробь от знака корня в знаменателе:

5. Докажите, что значение выражения есть число рациональное.

6. При каких значениях а дробь принимает наибольшее значение?

Вариант 2

1. Упростите выражение:

2. Сравните:

3. Сократите дробь:

4. Освободите дробь от знака корня в знаменателе:

5. Докажите, что значение выражения есть число рациональное.

6. При каких значениях х дробь принимает наибольшее значение?

Вариант 3

1. Упростите выражение:

2. Сравните:

3. Сократите дробь:

4. Освободите дробь от знака корня в знаменателе:

5. Докажите, что значение выражения есть число рациональное.

6. При каких значениях х дробь принимает наибольшее значение?

Вариант 4

1. Упростите выражение:

2. Сравните:

3. Сократите дробь:

4. Освободите дробь от знака корня в знаменателе:

5. Докажите, что значение выражения есть число рациональное.

6. При каких значениях р дробь принимает наибольшее значение?

Решение вариантов контрольной работы

Вариант 1

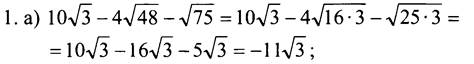
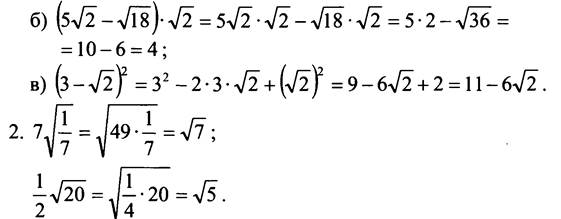
Так как √7 > √5, то

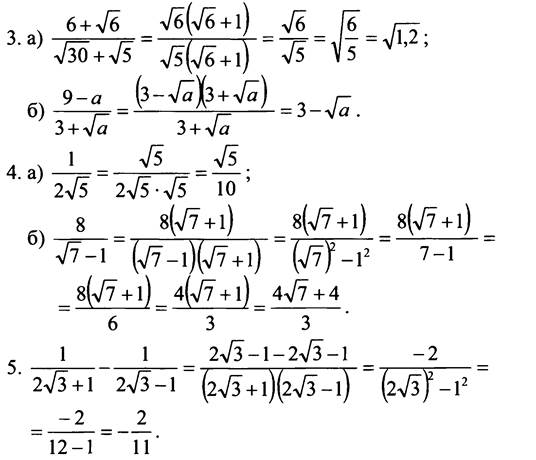
Значит, значение исходного выражения есть число рациональное.

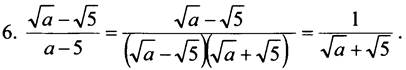
Выражение √а + √5 принимает положительные значения при всех допустимых значениях а.

Дробь будет наибольшей, если её знаменатель - наименьший, а выражение √а + √5 принимает наименьшее значение при а = 0.

Ответ: при а = 0.

Вариант 2

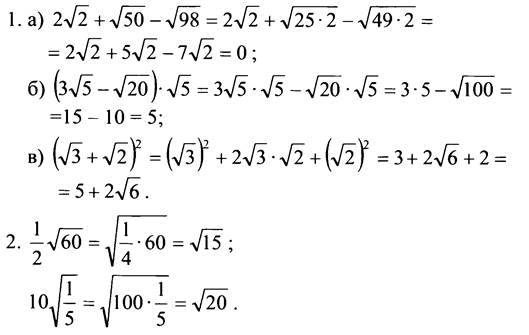
Так как √15 < √20, то

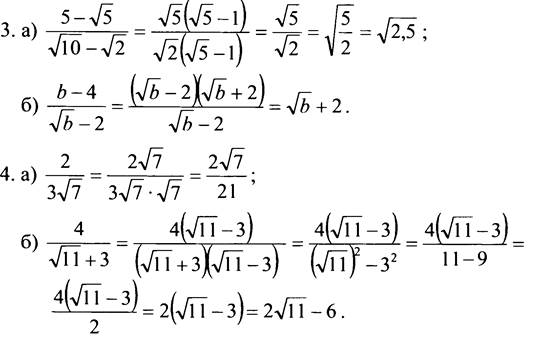
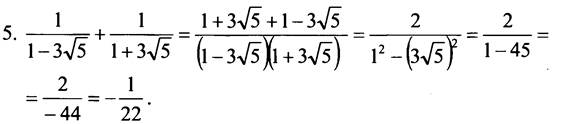
Значит, значение исходного выражения есть число рациональное.

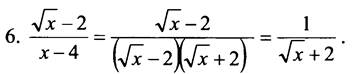
Выражение √х + 2 принимает положительные значения при всех допустимых значениях х.

Дробь будет наибольшей, если её знаменатель - наименьший, а выражение √x + 2 принимает наименьшее значение при х = 0.

Ответ: при х = 0.

Вариант 3

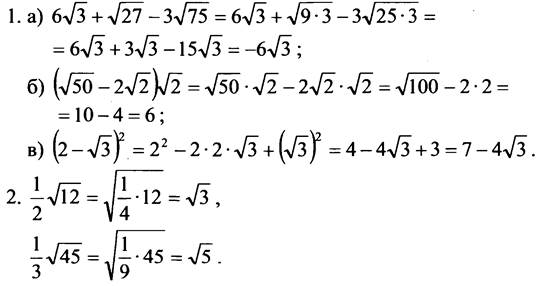
Так как √3 < √5, то

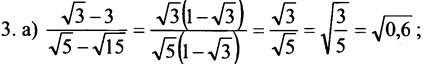
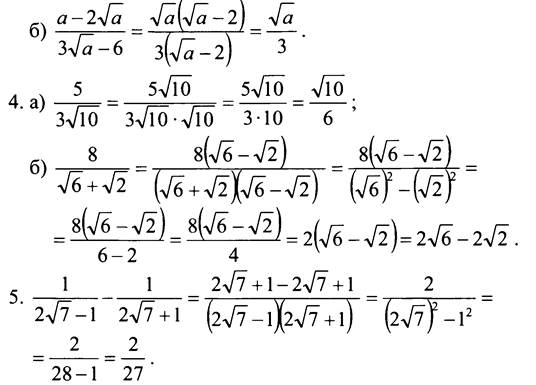
Значит, значение исходного выражения есть число рациональное.

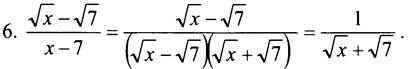
Выражение √x + √7 принимает положительные значения при всех допустимых значениях х.

Дробь будет наибольшей, если её знаменатель - наименьший, а выражение √x + √7 принимает наименьшее значение при х = 0.

Ответ: при х = 0.

Вариант 4

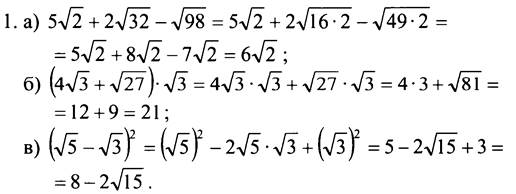
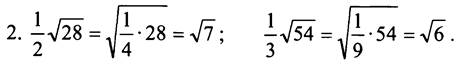
Так как √7 > √6, то

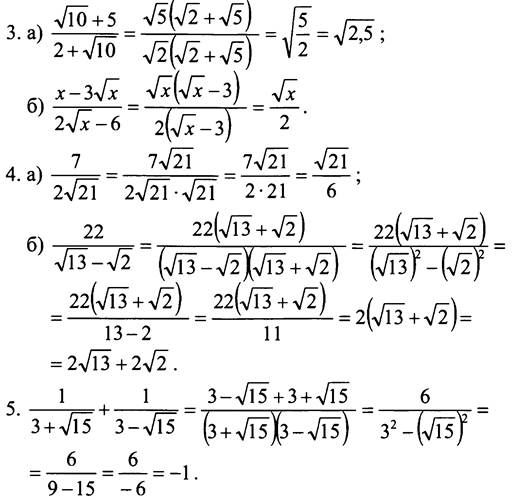
Значит, значение исходное выражение есть число рациональное.

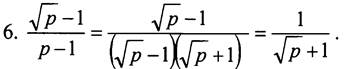
Выражение √p + 1 принимает положительные значения при всех допустимых значениях р. Дробь будет наибольшей, если её знаменатель - наименьший, а выражение √p + 1 принимает наименьшее значение при р = 0.

Ответ: при р = 0.