ОПРЕДЕЛЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ - КВАДРАТНЫЕ УРАВНЕНИЯ

Цели: ввести понятия квадратного уравнения, приведенного квадратного уравнения, неполного квадратного уравнения; формировать умения записывать квадратное уравнение в общем виде, различать его коэффициенты.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Является ли число а корнем уравнения:

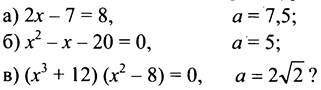
2. Найдите корни уравнения:

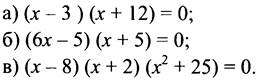
III. Объяснение нового материала.

Для введения понятия квадратного уравнения используется задача, при решении которой появляется уравнение, еще не известное учащимся. Возникает проблемная ситуация: мы не можем решить практическую задачу, так как пока не умеем решать уравнения нового вида. На этом уроке можно просто указать, какие корни имеет полученное уравнение, и сообщить, что такое уравнение называется квадратным.

На доску выносится запись:

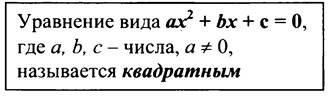
Далее рассматривается вопрос о коэффициентах квадратного уравнения. Число а называется первым коэффициентом, число b - вторым коэффициентом и число с - свободный член. Особое внимание обращаем, что число а не может быть равным нулю, так как в этом случае уравнение примет вид bх + с = 0, а это линейное уравнение.

Числа b и с, в отличие от а, могут быть и равными нулю. Если хотя бы одно из них равно нулю, то уравнение называется неполным. Можно предложить учащимся самостоятельно выписать виды неполных квадратных уравнений:

b	с	Уравнение
0	X	ах2 + с = 0
X	0	ах2 + bх = 0
0	0	ах2 = 0

Для усвоения понятия квадратного уравнения и его коэффициентов следует предложить учащимся следующее задание: Укажите, какие из данных уравнений являются квадратными, объясните ответ:

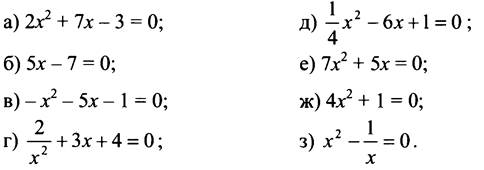
Затем определяется, какое квадратное уравнение называется приведенным, приводятся примеры.

IV. Формирование умений и навыков.

На этом уроке основное внимание следует уделить тому, чтобы учащиеся усвоили понятие квадратного уравнения, могли выделять его из множества уравнений, называть коэффициенты, преобразовывать неприведённое квадратное уравнение в приведённое, овладели соответствующей терминологией.

Уравнение	Коэффициенты
	а	b	с
3х2 + 7х - 6 = 0
- 5x2 + 2х + 4 = 0
15х - х2 = 0
7х2 = 0
3x - x2 + 19 = 0
2x2 – 11 = 0
2/3х2 - 2х = 0
х2 + 2 - x = 0

2. Составьте квадратное уравнение по его коэффициентам:

3. Приведите уравнение к виду ах² + bх + с = 0:

4. Какое из чисел 1; -3 является корнем данного уравнения?

5. Какие из данных уравнений являются приведёнными; неполными?

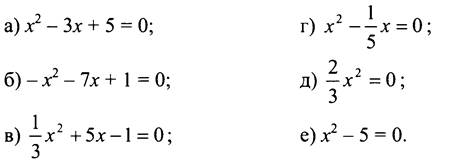
6. Преобразуйте квадратное уравнение в приведённое:

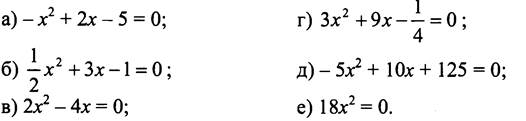
V. Итоги урока.

- Какое уравнение называется квадратным?

- Может ли коэффициент а в квадратном уравнении быть равным нулю?

- Является ли уравнение 3х² - 7 = 0 квадратным? Назовите коэффициенты этого уравнения.

- Какое квадратное уравнение называется неполным? Приведённым? Приведите примеры.

- Как преобразовать неприведённое квадратное уравнение в приведённое?

Домашнее задание: № 512, 513.

- Приведите уравнение к виду ах² + bх + с = 0.