РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ - КВАДРАТНЫЕ УРАВНЕНИЯ

Цель: продолжить формирование умения решать дробные рациональные уравнения по алгоритму.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Разложите на множители:

2. Решите уравнение:

III. Проверочная работа.

Вариант 1

Решите уравнения:

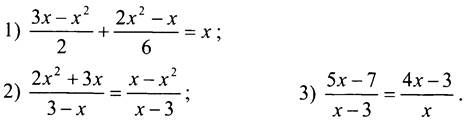
Вариант 2

Решите уравнения:

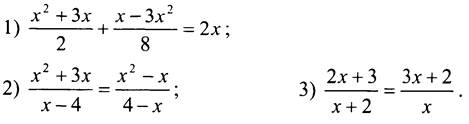
IV. Формирование умений и навыков.

На этом уроке отрабатывается умение находить общий знаменатель дробей, выполнив предварительно разложение знаменателей дробей, входящих в уравнение, вынесением общего множителя либо по формулам сокращенного умножения.

№ 603.

По теореме, обратной теореме Виета, x₁ = -9, x₂ = 1.

Ответ:

№ 605.

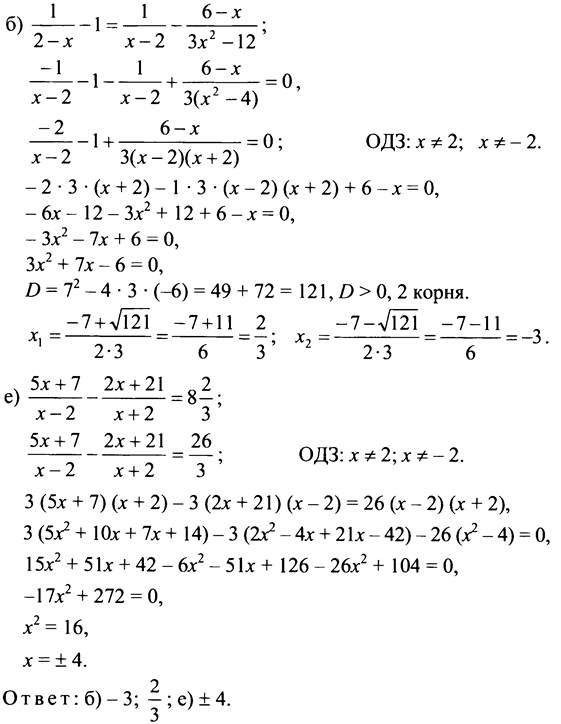
№ 604 (б).

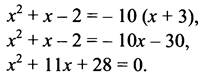
По теореме, обратной теореме Виета, x₁ = -4; х₂ = -7.

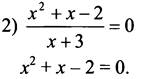
По теореме, обратной теореме Виета, х₁ = -2; х₂ = 1.

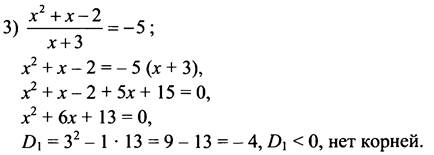
Ответ: 1) при х = -4 или х = -7; 2) при х = -2 или х = 1; 3) нет решений.

№ 606.

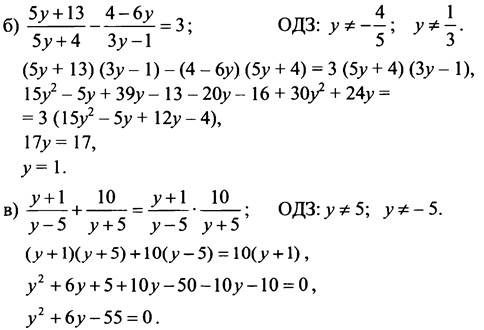
По теореме, обратной теореме Виета, у₁ = 5; у₂ = -11.

Ответ: б) 1; в) - 11.

№ 607.

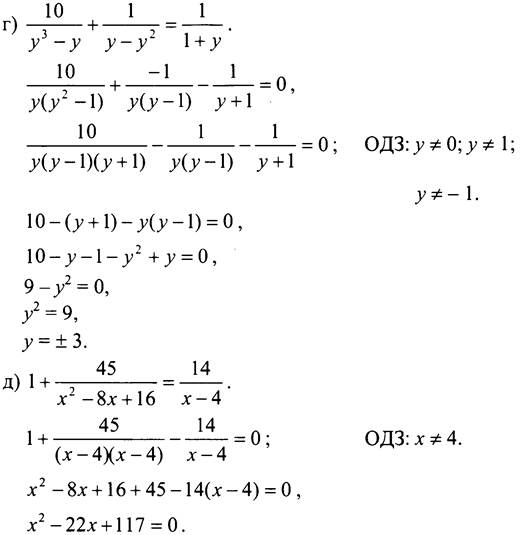
По теореме, обратной теореме Виета, x₁ = 9, x₂ = 13.

Ответ: г) ±3; д) 9; 13.

V. Итоги урока.

- Сформулируйте алгоритм решения дробного рационального уравнения.

- Как находится общий знаменатель дробей, входящих в запись дробно рационального уравнения?

- Какими способами можно исключить “посторонние” корни дробного уравнения?

Домашнее задание: № 603 (б, е), 605 (в, г), 606 (а, г), 607 (в, е).