Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
СОСТАВЛЕНИЕ ДРОБНОГО РАЦИОНАЛЬНОГО УРАВНЕНИЯ ПО УСЛОВИЮ ЗАДАЧИ - КВАДРАТНЫЕ УРАВНЕНИЯ
Цели: формировать умение составлять дробное рациональное уравнение по условию текстовой задачи и решать его.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Решите уравнение:

2. Заполните таблицу.
|
V |
t |
5 |
|
60 км/ч |
1,5 ч |
|
|
5 км/ч |
200 м |
|
|
45 мин |
1 км |
|
|
80 км/ч |
15 мин |
|
|
20 м/с |
2 км |
III. Проверочная работа.
Вариант 1
Найдите корни уравнений:
![]()
Вариант 2
Найдите корни уравнений:
![]()
IV. Объяснение нового материала.
Учащиеся уже знакомы с алгебраическим методом решения текстовых задач. Единственное отличие от ранее решаемых задач в том, что математической моделью будет являться дробное рациональное уравнение. Это можно продемонстрировать, используя примеры, разобранные в учебнике. При этом основное внимание следует уделять процессу перевода условия задачи на математический зык.
Затем следует ещё раз напомнить учащимся основные этапы решения текстовой задачи алгебраическим методом:
1-й этап. Анализ условия задачи и его схематическая запись.
2-й этап. Перевод естественной ситуации на математический язык (построение математической модели: введение переменной и составление дробного рационального уравнения).
3-й этап. Решение полученного уравнения.
4-й этап. Интерпретация полученного результата.
Первые два этапа являются для учащихся наиболее сложными, поэтому на этом уроке основной целью является формирование у учащихся умения составлять дробное рациональное уравнение по условию задачи.
V. Формирование умений и навыков.
Большая часть урока должна быть посвящена анализу условий задач, их схематичной записи, обоснованию выбора переменной и составлению уравнений. Решение самих уравнений можно также предлагать учащимся для самостоятельной работы.
№ 617.
Анализ: 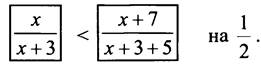
Пусть х - числитель обыкновенной дроби, тогда (х + 3) — её знаменатель. Увеличив числитель на 7, а знаменатель на 5, мы получили дробь ![]() Зная, что дробь увеличилась на 1/2, составим уравнение:
Зная, что дробь увеличилась на 1/2, составим уравнение:
![]()
Общий знаменатель 2(х + 3)(х + 8).
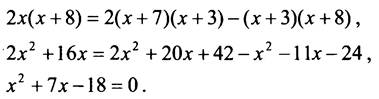
По теореме, обратной теореме Виета, x1 = 2, x2 = -9. Смыслу задачи удовлетворяет только х = 2, тогда дробь равна 2/5.
Ответ: 2/5.
Обращаем внимание учащихся, что уравнение исходное можно было записать и по-другому:
![]() (из большего значения вычитаем меньшее и получаем разницу) или
(из большего значения вычитаем меньшее и получаем разницу) или ![]()
№ 619.
Анализ:
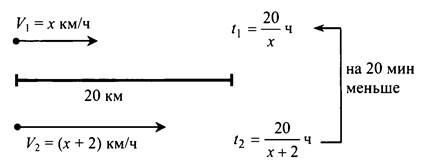
Пусть х км/ч - скорость лыжника, тогда (х + 2) км/ч - скорость второго лыжника. Первый лыжник затратил времени 20/x ч, второй - ![]() ч. Зная, что второй лыжник затратил на 20 мин, или 1/3 ч, меньше первого, составим уравнение:
ч. Зная, что второй лыжник затратил на 20 мин, или 1/3 ч, меньше первого, составим уравнение:
![]()
3x(х + 2) - общий знаменатель.
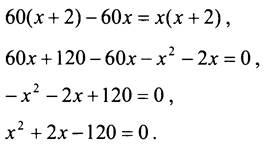
По теореме, обратной теореме Виета, х1 = -12, x2 = 10. Корень х = -12 не удовлетворяет условию задачи. Значит, 10 км/ч - скорость второго лыжника.
Ответ: 10 км/ч; 12 км/ч.
№ 621.
Анализ:
|
V, км/ч |
U ч |
S, км |
|
|
По расписанию |
x |
|
720 |
|
В действительности |
х + 10 |
720 |
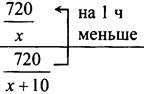
Пусть х км/ч - скорость поезда по расписанию, тогда (х + 10) км/ч - действительная скорость поезда. ![]() - время, которое должен был идти поезд по расписанию, а
- время, которое должен был идти поезд по расписанию, а ![]() - время, затраченное поездом в действительности. Зная, что поезд затратил на 1 ч меньше, чем должен был по расписанию, составим уравнение:
- время, затраченное поездом в действительности. Зная, что поезд затратил на 1 ч меньше, чем должен был по расписанию, составим уравнение:
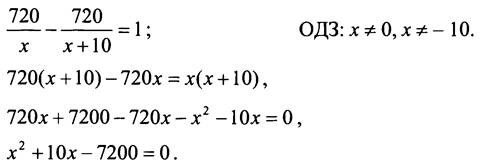
По теореме, обратной теореме Виета, х1 = -90, x2 = 80. Корень х = -90 не удовлетворяет условию задачи.
Ответ: 80 км/ч.
№ 623.
Анализ:
|
Цена, р. |
Кол-во, шт. |
Стоимость, р. |
|
|
“Надежда” |
x |
|
240 |
|
“Удача” |
х- 5 |
240 |
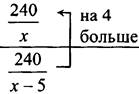
Пусть х р. - цена лотерейного билета “Надежда”, тогда (х - 5) р. - цена лотерейного билета “Удача”. Андрей купил ![]() билетов лотереи “Надежда”, и
билетов лотереи “Надежда”, и ![]() билетов лотереи “Удача” он мог бы купить. Зная, что Андрей мог бы купить на 4 билета лотереи “Удача” больше, составим уравнение:
билетов лотереи “Удача” он мог бы купить. Зная, что Андрей мог бы купить на 4 билета лотереи “Удача” больше, составим уравнение:
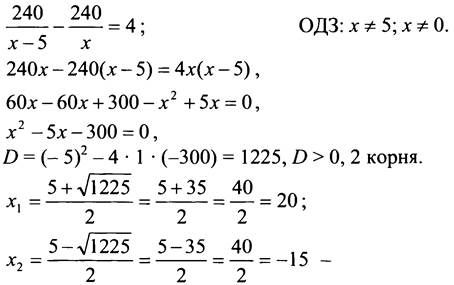
не удовлетворяет условию задачи.
Ответ: 20 р.
VI. Итоги урока.
- Каковы этапы решения задач на составление дробного рационального уравнения?
- Каков алгоритм решения дробного рационального уравнения?
- Как проводится интерпретация полученных решений? В каких случаях полученные корни уравнения могут не удовлетворять условию задачи?
Домашнее задание: № 618, 620, 624, 639.