РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ - КВАДРАТНЫЕ УРАВНЕНИЯ

Цель: формировать умение решать текстовые задачи с помощью дробных рациональных уравнений.

Ход урока

I. Организационный момент.

II. Устная работа.

Найдите:

а) 50 % от 42;

б) 1 % от 300;

в) 2 % от 200;

г) 10 % от 35;

д) 25 % от 280;

е) 20 % от 55;

ж) 50 % от 31;

з) 3 % от 90;

и) 10 % от 7;

к) 25 % от 84.

III. Проверочная работа.

Вариант 1

Числитель обыкновенной дроби на 4 меньше её знаменателя. Если к числителю этой дроби прибавить 19, а к знаменателю 28, то она увеличится на 1/5. Найдите эту дробь.

Вариант 2

Знаменатель несократимой обыкновенной дроби на 4 больше её числителя. Если числитель этой дроби увеличить на 2, а знаменатель - на 21, то дробь уменьшится на 1/4. Найдите эту дробь.

IV. Формирование умений и навыков.

На этом уроке следует разнообразить содержание текстовых задач. Следует прорешать задачи на движение; на работу; на концентрацию. Учащимся необходимо продемонстрировать важность этапа анализа условия задачи и удобство и универсальность таблиц и схем для записи связи исходных и требуемых величин.

№ 622.

Анализ:

	Урожайность, ц/га	Площадь, га	Урожайность, ц
Прошлый год	x		192
Этот год	х + 2		192

По условию меньше на 0,4 га.

Пусть х ц/га - урожайность пшеницы в хозяйстве в прошлом году, тогда (х + 2) ц/га - урожайность пшеницы в этом году. В прошлом году под пшеницу занято га, в этом га. Зная, что в этом году эта площадь была меньше на 0,4 га, составим уравнение:

не удовлетворяет условию задачи.

Ответ: 30 ц/га.

№ 625.

Анализ:

	Доля в оплате, шиллинг	Кол-во людей, чел.	Счет (сумма), шиллинг
По плану		x	175
В действительности		х - 2	175

В действительности больше на 10 шиллингов.

Пусть x человек обедало, тогда (x - 2) человек оплачивали поровну весь обед. шиллингов заплатил бы один человек, если бы деньги были у всех едоков, а шиллингов заплатил каждый человек с деньгами в действительности. Зная, что каждому пришлось уплатить на 10 шиллингов больше, составим уравнение:

По теореме, обратной теореме Виета, х₁ = 7, x₂ = -5 - не удовлетворяет условию задачи.

Ответ: 7 человек.

Перед решением задачи № 630 необходимо вспомнить, что такое концентрация вещества в растворе (сплаве, слитке, смеси и т. п.).

где k - концентрация вещества в процентах, m₁ - масса вещества, m - общая масса.

Также необходимо вспомнить, что для содержащегося вещества мы можем указывать как его относительное содержание в растворе (в процентах или в долях), так и абсолютное содержание (в граммах, тоннах, литрах и т. п.). Как правило, в текстовых задачах на концентрацию мы составляем уравнение по зависимости между абсолютным и относительным количеством вещества.

№ 630.

Анализ:

	Концентрация соли, %	Масса соли, г	Масса раствора, г
1 -й раствор		30	x
2-й раствор		30	х + 100

По условию меньше на 1 %.

Пусть х г - первоначальная масса раствора, тогда (х + 100) г - масса нового раствора. Концентрация соли первоначально составляла затем стала Зная, что концентрация соли снизилась на 1 %, составим уравнение:

не удовлетворяет условию задачи.

Ответ: 500 г.

Перед решением задач № 627, 629 нужно вынести на доску табличку:

В стоячей воде	V = Vсобст
По течению	V = Vсобст + Vтеч
Против течения	V = Vсобст - Vтеч

В классе только проанализировать условие и составить уравнение. Уравнения дорешать дома.

№ 627.

Анализ:

	V, км/ч	t, ч	S, км
Против течения	х - 2		6
По озеру	х	15/x	15

По условию 15/x больше на 1 час.

Пусть х км/ч - собственная скорость лодки, тогда (х - 2) км/ч - скорость лодки при движении против течения. ч турист плыл на лодке против течения, а 15/x ч - он плыл на лодке по озеру. Зная, что на путь по озеру он затратил на 1 час больше, составим уравнение:

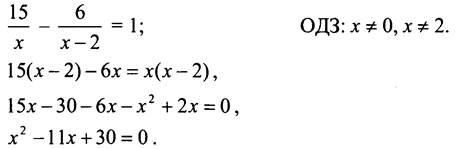
По теореме, обратной теореме Виета, x₁ = 5, х₂ = 6. Оба корня удовлетворяют условию задачи.

Ответ: 5 км/ч или 6 км/ч.

№ 629.

Анализ:

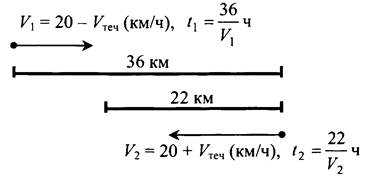
По условию t₁ + t₂ = 3 ч.

Пусть х км/ч - скорость течения реки, тогда против течения катер шёл со скоростью (20 - х) км/ч, а по течению - (20 + х) км/ч. Против течения он шел ч, а по течению ч. Зная, что на весь путь катер затратил 3 часа, составим уравнение:

не удовлетворяет условию задачи.

Ответ: 2 км/ч.

V. Итоги урока.

- Назовите основные этапы решения текстовой задачи алгебраическим методом.

- Какие способы схематичной записи условия задачи вы знаете?

- В чём особенности решения задач на концентрацию?

- В чём особенности решения задач на движение, если в тексте идёт речь о движении по реке?

Домашнее задание: № 626, 628, 627 (дорешать уравнение), 629 (дорешать уравнение).