Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ДРОБИ - НЕРАВЕНСТВА
Цели: разобрать способ решения неравенств с одной переменной, содержащих дроби; продолжить формирование навыков решения неравенств путём перехода к равносильным неравенствам.
Ход урока
I. Организационный момент.
II. Математический диктант.
Вариант 1 [Вариант 2]
1. Запишите числовой промежуток, служащий множеством решений неравенства х ≤ 3. [у > -8]
2. Запишите неравенство, множеством решений которого служит промежуток (-3; +∞). [(-∞; 7)]
3. Решите неравенство:
![]()
4. Решите неравенство:
![]()
Ответы:
|
Вариант 1 |
Вариант 2 |
|
|
1 |
(-∞; 3] |
(-8; +∞) |
|
2 |
x > -3 |
х < 7 |
|
3 |
|
|
|
4 |
(-∞; -0,8) |
(-∞; -4) |
III. Объяснение нового материала.
Проверить выполнение домашнего задания: № 871 (а). Рассмотреть по учебнику пример 3 на с. 178.
IV. Формирование умений и навыков.
В предлагаемых заданиях необходимо уметь находить общий знаменатель дробей, входящих в запись уравнения, затем домножить обе части неравенства на общий знаменатель и решить полученное неравенство. Также следует уделять внимание изображению множества решений на координатной прямой.
№ 849.
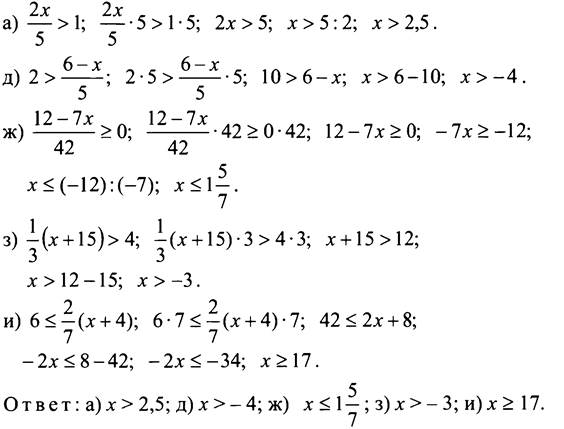
№ 851.
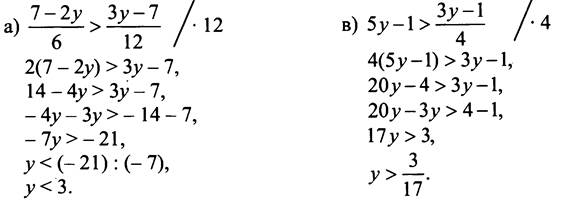
Ответ: а) при у < 3; в) при у > 3/17.
№ 852.
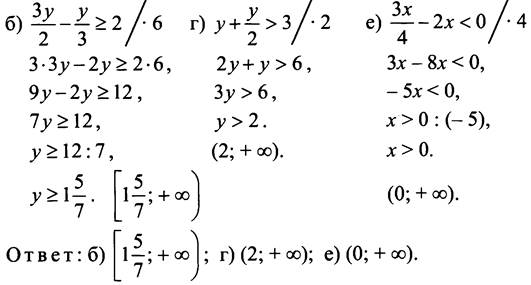
№ 853.
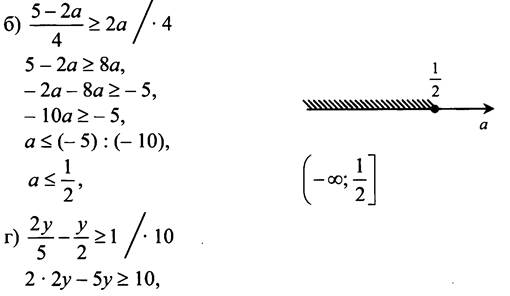
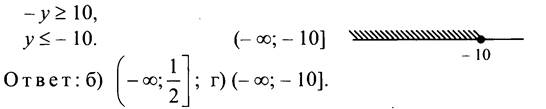
№ 854.

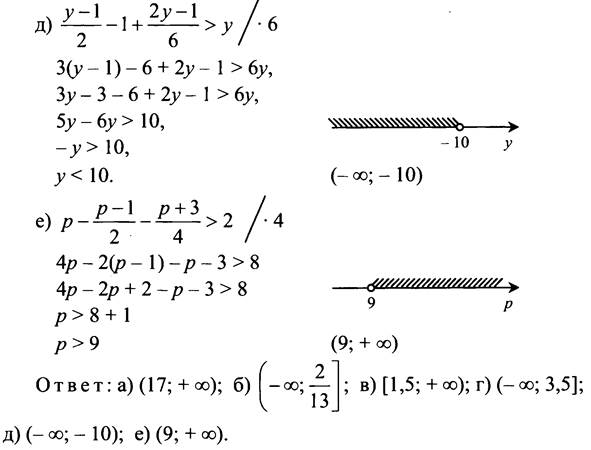
№ 856.
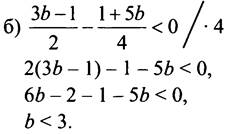
Ответ: при b < 3.
V. Итоги урока.
- Что значит решить неравенство с одной переменной?
- Каков алгоритм решения неравенства с одной переменной, содержащего дробь?
Домашнее задание: № 850, 851 (б, г), 852 (а, в, д), 855, 856 (а).