Алгебра поурочные планы 8 класс - по учебнику Ю. Н. Макарычева
РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ - НЕРАВЕНСТВА
Цель: продолжить формировать умение решать системы неравенств с одной переменной путем равносильных преобразований неравенств.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Является ли число 6 решением системы неравенств:

2. Решите систему неравенств:
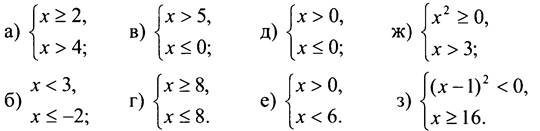
III. Формирование умений и навыков.
На этом уроке учащимся предлагаются для решения более сложные системы неравенств. Кроме того, задания сформулированы таким образом, что требуется не только найти решение системы, но и проверить выполнение каких-либо дополнительных условий.
№ 822 (б, г).
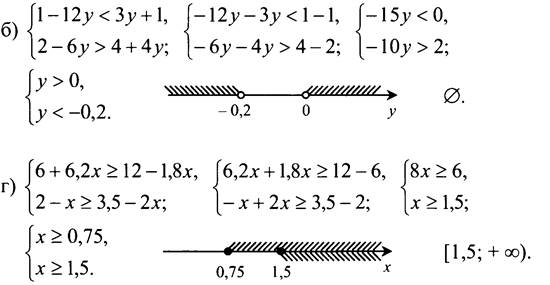
Ответ: б) нет решений; г) [1,5; +∞).
№ 883 (б, г).
Допустимы те значения переменной, при которых подкоренные выражения неотрицательны:
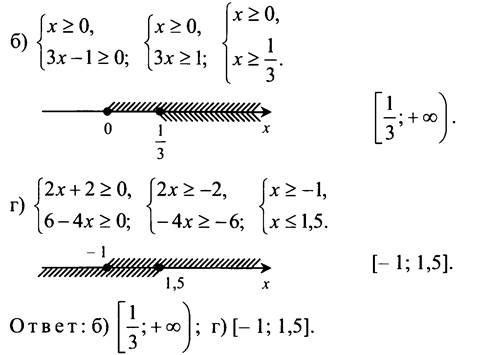
№ 884 (б).
б) В область определения функции ![]() входят те значения х, для которых подкоренные выражения неотрицательны и знаменатель дроби не обращается в нуль.
входят те значения х, для которых подкоренные выражения неотрицательны и знаменатель дроби не обращается в нуль.
![]()
Знаменатель равен нулю, если
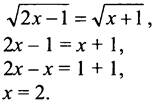
Значит, из области определения функции необходимо исключить х = 2.
![]()
Ответ: [0,5; 2) ∪ (2; +∞).
№ 886 (б, г).
![]()

№ 887 (б, г).
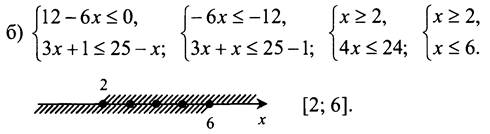
Целыми решениями являются: 2; 3; 4; 5; 6.
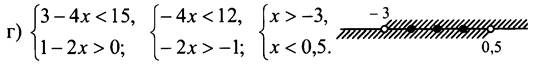
Целыми решениями являются: -2; -1; 0.
Ответ: б) 2; 3; 4; 5; 6; г) -2; -1; 0.
IV. Проверочная работа.
Вариант 1
Решите систему неравенств:
![]()
Вариант 2
Решите систему неравенств:
![]()
V. Итоги урока.
- Что называется решением системы неравенств?
- Что значит решить систему неравенств?
- Каков алгоритм решения системы неравенств?
- Сколько решений может иметь система неравенств?
Домашнее задание: № 881, 883 (а, в), 885, 886 (а, в), 888.