ввести понятие криволинейной трапеции и рассмотреть ей площадь - ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ - ИНТЕГРАЛ - 1-е полугодие

Цели: ввести понятие криволинейной трапеции и рассмотреть ей площадь.

Ход урока

I. Итоги и анализ контрольной работы. Учащиеся, не справившиеся с работой, получают индивидуальную карточку № 2.

II. Объяснение нового материала

1. Ввести определение криволинейной трапеции.

2. Рассматриваем рисунки на доске. Выясняем, какие из предложенных являются криволинейными трапециями.

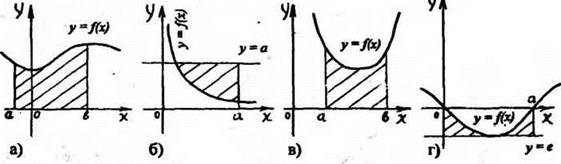
Рис. 3

3. Доказательство формулы S = F(b) – F(a).

III. Закрепление изученного материала. № 353 (а; б; г).

IV. Итоги урока

V. Домашнее задание: п. 29; № 353 (b), № 354 (в; г).

Карточка № 2

1. Найдите первообразные функций:

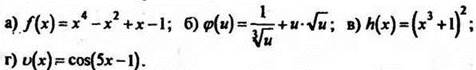
Решение

Для нахождения первообразных функций воспользуемся таблицей первообразных.

а) x5/5 - одна из первообразных функции х4; x3/3 - одна из первообразных функции х2; x2/2 - одна из первообразных функции х; х - одна из первообразных функции 1.

По правилу 1 нахождения первообразных 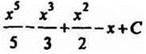- первообразная функции f(х);

б) функцию (u) запишем в виде

- одна из первообразных функции u1/3; - одна из первообразных функции u3/2; 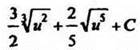- первообразная функции (u);

X7/7 - одна из первообразных функции х6; x4/4 - одна из первообразных функции х3; х - одна из первообразных функции 1.

По правилам 1 и 2 нахождения первообразных - первообразная функции h(х);

sinu - одна из первообразных функции cosu; - первообразная функции (х).

2. Повторите формулы первообразных функций и правила нахождения первообразны.

Задания:

1. Применяя правило 1, найдите первообразную функции

2. Применяя правила 1 и 2, найдите первообразную функции:

3. Применяя правило 3, найдите первообразную функции:

4. Найдите первообразную функции: