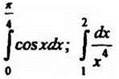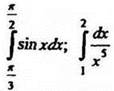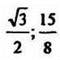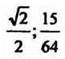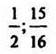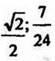упражнять в вычислении площади криволинейных трапеций и проверить степень приобретения навыка - ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА - ИНТЕГРАЛ - 1-е полугодие

Цели: упражнять в вычислении площади криволинейных трапеций и проверить степень приобретения навыка.

Ход урока

I. Проверка домашнего задания

Вопросы для фронтальной работы.

1. Запишите формулу Ньютона-Лейбница.

2. Что представляет геометрически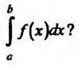

3. Вычислите:

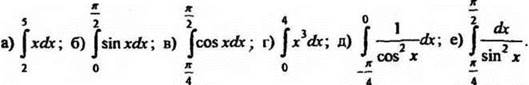
Ответы: а) 10,5; б) 1; в) /2; г) 64; д) 1; е) 1.

II. Решение упражнений

1. № 360 (г).

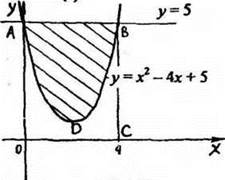
Рис. 12

1) Найдём пределы интегрирования.

х2 - 4х + 5 - 5; х2 - 4х = 0; х = 0 или х = 4;

2) Искомая площадь может быть получена как разность площадей прямоугольника АВСО и криволинейной трапеции AOCBD.

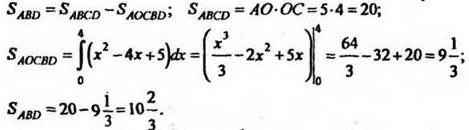
2. Работа группами. № 361 (б, г), № 364 (а, б).

Группа слабых работает по карточке № 3 с помощью учителя.

Карточка № 3

1). Вычислите площадь заштрихованной фигуры.

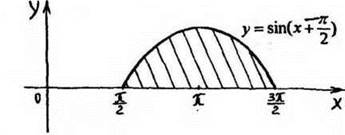
Ответ: 2.

2). Вычислите площадь криволинейной трапеции, ограниченной линиями у = х2, y = 4, х = -2, х = 2. Ответ:

3). Вычислите площадь фигуры, ограниченной линиями у = х2 +1, у = 5. Ответ:

III. Самостоятельная работа.

Программированный контроль.

Задание		Ответ
Вариант I	Вариант II	1	2	3	4
Вычислите:
Вычислите площадь фигуры, ограниченной линиями: y = х2; y = 0; х = 2.	y = х3; y = 0; х = 2.	4	8		2

Верный ответ: вариант I - 2, 4, 3; вариант II - 3, 2, 1.

IV. Итоги урока

V. Домашнее задание: п. 30 (выучить к зачёту по § 7-8 теоретический материал); № 361 (а; в), № 362; повторить уравнение касательной п. 19.