проверить знания и умения учащихся по теме «Первообразная и интеграл» - ПРИМЕНЕНИЕ ИНТЕГРАЛА - ИНТЕГРАЛ - 1-е полугодие

Цели: проверить знания и умения учащихся по теме «Первообразная и интеграл».

Ход урока

I. Вопросы для фронтального опроса

1. Сформулируйте определение первообразной.

2. Какие из функций являются первообразными для функции

3. Докажите, что функция является первообразной функции на промежутке (0;∞).

4. Сформулируйте основное свойство первообразной. Как геометрически интерпретируется это свойство?

5. Для функции найдите первообразную, график которой проходит через точку . (Ответ: F(x) = tgx + 2.)

6. Сформулируйте правила нахождения первообразной.

7. Сформулируйте теорему о площади криволинейной трапеции.

8. Запишите формулу Ньютона-Лейбница.

9. В чём заключается геометрический смысл интеграла?

10. Приведите примеры применения интеграла.

II. Организация учащихся на зачёт (письменный или с привлечением консультантов)

III. Зачёт

Карточка 1

1. Сформулируйте определение первообразной. Приведите примеры.

2. Дня функции f(x) = sinx + 2cosx найдите первообразную, график которой проходит через точку А

3. Вычислите площадь фигуры, ограниченной линиями:

Карточка 2

1. Докажите основное свойство первообразной.

2. Найдите общий вид первообразной для функции

3. Вычислите площадь фигуры, ограниченной линиями:

Карточка 3 .

1. Докажите три правила нахождения первообразных.

2. Вычислите: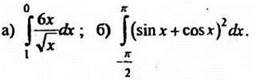

3. Вычислите плошадь фигуры, ограниченной линиями:

Карточка 4

1. Пусть криволинейная трапеция ограничена графиком непрерывной функции f(х) > 0, прямыми х = а, х = b и отрезком [a;b] оси абсцисс. S - площадь трапеции. Разъясните смысл равенства S'(x) = f(х).

2. Вычислите: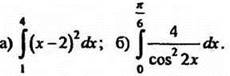

3. Вычислите площадь фигуры, ограниченной линиями:

Карточка 5

1. Пусть криволинейная трапеция ограничена графиком непрерывной функции F(х) > 0, прямыми х = а, х = b и отрезком [а;b] оси абсцисс; S – плошадь трапеции. Разъясните смысл равенства S(x) = F(x) - F(a) и S = F(b) – F(a).

2. Докажите, что есть первообразная для функции на промежутке (0;∞).

3. Вычислите площадь фигуры, ограниченной линиями:

Карточка 6

1. Запишите формулу Ньютона-Лейбница. Разъясните ей смысл.

2. Для функции f(x) = 6sin4x найдите первообразную, график которой проходит через точку B (-/3;0).

3. Вычислите площадь фигуры, ограниченной линиями:

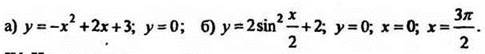
IV. Итоги урока

V. Домашнее задание: подготовка к контрольной работе; № 363, № 367, № 368, № 366 (b), № 365 (a).