закрепить правила вычисления производных; способствовать выработке навыков в применении производной к исследованию функций и нахождении наибольшей) и наименьшего значения функции - ПОВТОРЕНИЕ: ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ, ПРОИЗВОДНЫЕ ФУНКЦИЙ у = sinx, у = соsx, у = tgx, у = ctgx, у = xn, ГДЕ n∈Z, n ≠ -1. ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ, ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ - 1-е полугодие

Цели: закрепить правила вычисления производных; способствовать выработке навыков в применении производной к исследованию функций и нахождении наибольшей) и наименьшего значения функции.

Ход урока

I. Математический диктант (10 -15 мин)

Вариант I

1. Найдите производные функций:

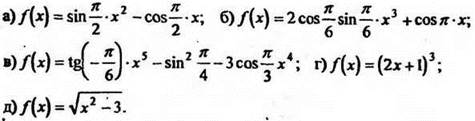
2. Решите методом интервалов неравенство:

3. Найти промежутки возрастания и убывания функции; найти точки экстремума функции: f(х) = 4х3 + 12х.

Вариант I.

1. Найдите производные функций:

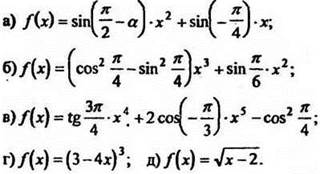
2. Решите методом интервалов неравенство:

3. Найти промежутки возрастания и убывания функции; найти точки экстремума функции: f(х) = х3 - 3х.

II. Решение задач

1. Сформулируйте правило нахождения наибольшего и наименьшего значений функции на отрезке.

2. Найти наименьшее значение функций на заданных отрезках:

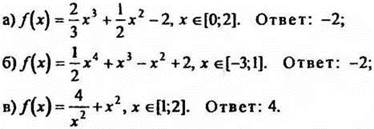
3. Задача 1. Число 64 представлено в виде суммы двух положительных слагаемых так, что сумма их квадратов минимальна. Найти эти слагаемые. Ответ: 32; 32.

4. Задача 2. Найти положительное число, сумма которого со своей обратной величиной имеет наименьшее значение. Ответ: 1.

5. Найти значения функций в точках максимума:

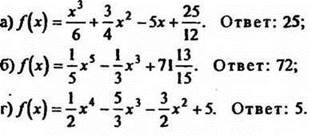
6. Самостоятельно решить (с последующей проверкой).

Вычислить значения производных функций при заданных значениях аргумента:

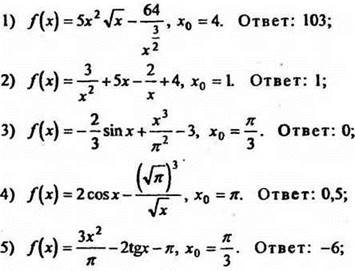
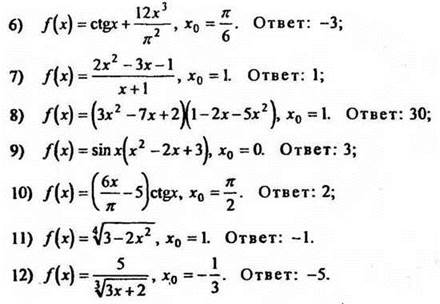
III. Итоги урока

IV. Домашнее задание: повторить материал § 4, 5, 6; решить на стр. 295 № 238, № 240; на стр. 297 № 264, № 265.