Алгебра и начала анализа для учащихся 11 класса поурочные планы
повторить производную функции у = хn, где n∈Z, n ≠ -1; закрепить правила вычисления производных тригонометрических функций; вырабатывать навык применения производной - ПОВТОРЕНИЕ: ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ, ПРОИЗВОДНЫЕ ФУНКЦИЙ у = sinx, у = соsx, у = tgx, у = ctgx, у = xn, ГДЕ n∈Z, n ≠ -1. ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ, ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ - 1-е полугодие
Цели: повторить производную функции у = хn, где n![]() Z, n ≠ -1; закрепить правила вычисления производных тригонометрических функций; вырабатывать навык применения производной.
Z, n ≠ -1; закрепить правила вычисления производных тригонометрических функций; вырабатывать навык применения производной.
Ход урока
I. Устная работа
1. Найдите производные функций:
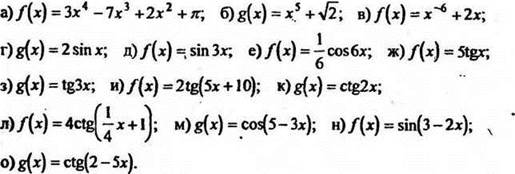
2. При каких значениях х выполняется неравенство f(х) < g'(x), если f(x) = sinx и g(x) = 5x + 1? Ответ: при любых значениях х.
3. Даны функции h(х) = cosx + 5 и f(x) = -2х -1. Определите, при каких значениях переменной х выполняется неравенство h'(х) < f(х).
Ответ: таких значений нет.
4. Какую прямую называют касательной к графику функции f в точке (x0;f(x0))?
5. В чём состоит геометрический смысл производной?
6. Напишите уравнение касательной к графику функции f в точке (x0;f(x0)).
7. Сформулируйте признак возрастания (признак убывания) функции.
8. Какую точку называют критической точкой функции? Сформулируйте признак максимума (минимума) функции.
II. Выполнение упражнений
1. Составить уравнение касательной к графику функции в точках с заданными абсциссами:
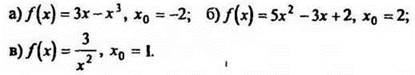
2. Будет ли касательная к графику функции у = х3 —х в точке х = 0 параллельна прямой: ![]()
Ответ: а) нет; б) да; в) нет; г) да.
3. В какой точке параболы y = 0,5x2 - х касательная к ней наклонена к оси абсцисс под углом ![]() /4? Ответ: (2;0).
/4? Ответ: (2;0).
4. В какой точке касательная к графику функции у = -х2 + 4x - 3 параллельна оси абсцисс? Ответ: (2; 1).
5. В интервале [0;![]() ) найти абсциссу течки, в которой касательная к кривой у = 4sin3x - 6х + 7 параллельна прямой y = 2 – 6x.
) найти абсциссу течки, в которой касательная к кривой у = 4sin3x - 6х + 7 параллельна прямой y = 2 – 6x.
6. Найти экстремумы функций:
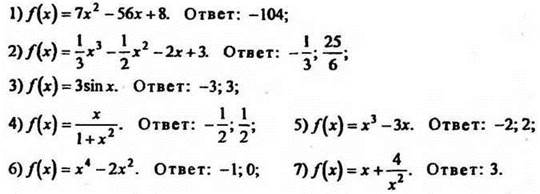
III. Итоги урока
IV. Домашнее задание: повторить п. 22 - 25 из § 6; решить на стр. 294 № 231, № 232 (в; г).