в ходе выполнения упражнений закрепить знание решения логарифмических уравнений; рассмотреть решение систем логарифмических уравнений - РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ - ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ - 2-е полугодие

Цели: в ходе выполнения упражнений закрепить знание решения логарифмических уравнений; рассмотреть решение систем логарифмических уравнений.

Ход урока

I. Устная работа

1. Какие уравнения называются логарифмическими?

2. Является ли уравнение lg5 + х lg6 = 3 логарифмическим.

3. Существует ли хотя бы одно значение х, при котором верно равенство lg(x+3) = lgх + lg3?

4. Записать область определения логарифмического уравнения loga f(x) = logb g(x) в виде системы неравенств.

5. Как решается уравнение, содержащее неизвестное и в основании, и в показателе степени, например хlgx = 10? .

6. Нужна ли проверка полученных корней фи решении логарифмических уравнений? Почему?

7. Решить уравнения:

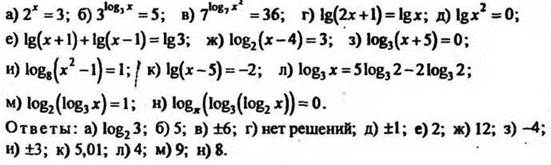
II. Выполнение упражнений

1. Объясняет учитель: решить уравнение

Решение

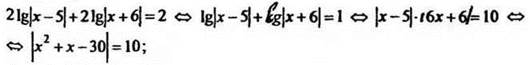
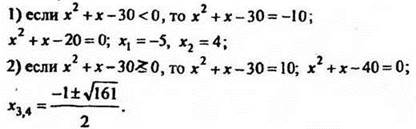
Проверка. Убеждаемся, что 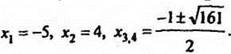являются корнями уравнения. Ответ: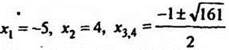

2. Решить уравнение

Решение

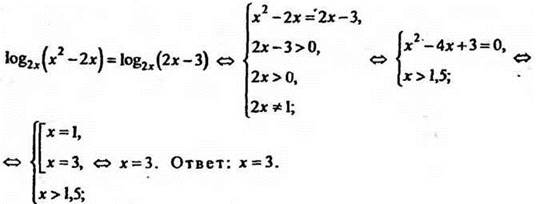
3. Решить уравнение

Решение

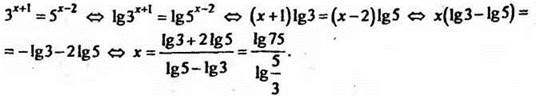
4. Решить уравнение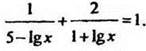

Решение

Найдём ОДЗ: х > 0; 5 – lgx ≠ 0; 1 + lgx ≠ 0, откуда х > 0; lgх ≠ 5; lgх ≠ -. Значит, 0 < х < 0,1; 0,1 < х < 100000; 100000 < х < +∞.

Заменим lgx = t, тогда относительно t уравнение примет вид: В результате решения находим t1 = 2, t2 = 3 или lgx = 2, х1 = 100; lgx = 3, x2 = 1000.

Ответ: х1, = 100; x2 = 1000.

5. Разобрать решение системы уравнений в примере 6 на стр. 234.

6. Решить № 521 (а, б).

7*. Решить систему уравнений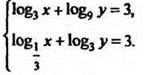

Решение

В каждом из уравнений системы перейдём к логарифмам по одному основанию 3. Получим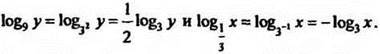

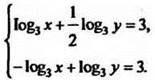
Складывая уравнения системы, получим

Отсюда y = 34 = 81. Подставляя y = 81 в первое уравнение системы, найдем значение х:

ОДЗ данной системы х > 0, у > 0, значит, 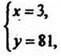является решением заданной системы.

III. Итоги урока

IV. Домашнее задание: п. 39; решить № 521 (в; г), N° 522 (б; в), № 523 (б), № 529 (а; в).